圓形

圓形有時叫圓，係圓嘅幾何圖形。圓形個中心叫圓心，而條邊嘅叫圓周。圓心同圓周之間，每點嘅直綫距離係一樣嘅，呢個距離就叫半徑。而一條直綫，由一圓周上一點，通過圓心到圓周另一邊，呢個就叫直徑。

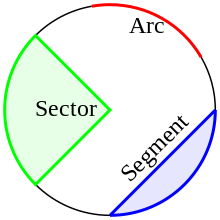
喺圓形上面任意篤兩點，然後用直線連埋，嗰條直線就叫做弦。將條弦向兩邊延長，就變咗做割線。如果一條直線同圓形只有一個交點，嗰條直線就叫做切線。圓周嘅一橛仔就係弧。弧嘅兩邊同兩條半徑組成扇形，而弧嘅兩邊同弦組成弓形。

圓心叫 $O$ 嘅話，噉個圓形可以寫成 $\odot O$ 。

方程同公式

圓形嘅方程可以寫做：

(x-h)^{2}+(y-k)^{2}=r^{2}

(標準式)

其中

r

係半徑，

(h,k)

係圓心嘅座標。

或

x^{2}+y^{2}+Dx+Ey+F=0

(一般式)

標準式同一般式嘅轉換係：

{\begin{aligned}&D=-2h\\&E=-2k\\&F=h^{2}+k^{2}-r^{2}\end{aligned}}

圓形嘅參數方程係：

{\begin{cases}x=r\cos t\\y=r\sin t\\\end{cases}},\ t\in [0,2\pi )

圓周長度 $=2\pi r$
圓面積 $=\pi r^{2}$

入面

\pi

係圓周率，係圓周同直徑嘅比例。

幾何特性

圓形有好多幾何特性（定理），下面會將啲特性逐個列出嚟。

對稱性

圓形有無限條對稱軸，都係穿過圓心嘅。有好多圓嘅性質都可以由佢嘅對稱性推出。

圓周上面是但一點都同圓心等距

如果有兩點 $A$ 同 $B$ 都係喺一個圓心係 $O$ 嘅圓形上面，噉樣嘅話 $OA=OB$ 。（定理縮寫：（半徑）/ $(\mathrm {radii} )$ ）

圓心去到弦又垂直於弦嘅直線平分弦

對於圓形裏面嘅是但一條弦 $AB$ ，如果一條經過圓心 $O$ 嘅直線同條弦垂直（而且當交點係 $C$ ，即係 $OC\perp AB$ ），噉嗰條直線就會平分條弦（ $AC=CB$ ）。（定理縮寫：（圓心至弦嘅垂線平分弦）/ $(\mathrm {line\ from\ centre} \perp \mathrm {chord\ bisects\ chord} )$ ）

圓心去到弦又平分弦嘅直線垂直於弦

對於圓形裏面嘅是但一條弦 $AB$ ，如果一條經過圓心 $O$ 嘅直線平分條弦（而且當交點係 $C$ ，即係 $AC=CB$ ），噉嗰條直線就會同條弦垂直（ $OC\perp AB$ ）。（定理縮寫：（圓心至弦中點嘅連線⊥弦）/ $(\mathrm {line\ from\ centre\ to\ mid}$ - $\mathrm {pt.\ of\ chord} \perp \mathrm {chord} )$ ）

等長嘅弦同圓心同距

對於同一個圓形裏面兩條一樣長嘅弦（ $AB$ 同 $CD$ ，中點分別係 $M$ 同 $N$ ），佢哋同圓心 $O$ 嘅距離一樣（ $OM=ON$ ）。（定理縮寫：（等長嘅弦同圓心同距）/ $(\mathrm {equal\ chords} ,\ \mathrm {equidistant\ from\ centre} )$ ）

同圓心同距嘅弦等長

對於同一個圓形裏面兩條一樣長同圓心同距嘅弦（ $AB$ 同 $CD$ ），佢哋嘅長度一樣（ $AB=CD$ ）。（定理縮寫：（同圓心同距嘅弦等長）/ $(\mathrm {chords\ equidistant\ from\ centre\ are\ equal} )$ ）

圓形

目錄

方程同公式

幾何特性