1 + 1 + 1 + 1 + ⋯

1 + 1 + 1 + 1 + ⋯，又可以寫做$\sum _{n=1}^{\infty }n^{0}$，$\sum _{n=1}^{\infty }1^{n}$或者直接啲$\sum _{n=1}^{\infty }1$，係一條發散級數，即係話佢對應嘅部份和數列唔能夠改斂去任何一個實數。$\sum _{n=1}^{\infty }1^{n}$可以睇做一條公比係1嘅幾何級數，同其他有理數公比（-1都除外）嘅幾何級數唔同，佢喺實數同任何p-進數入面都係發散嘅。喺擴展實數線入面，我哋可以寫

1 + 1 + 1 + 1 + ⋯

Smoothing 之後

Smoothing嘅漸近表現，條直線嘅y截距係$-2$。

$\sum _{n=1}^{\infty }1=+\infty$

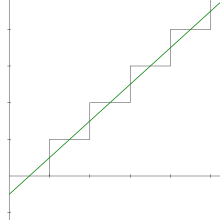
因為對應嘅部份和數列係單調無上界咁上升。

喺理論物理學嘅應用入面，每當見到n⁰嘅和嘅時候，都可以試吓將佢用zeta函數解析延拓嚟演繹。黎曼zeta函數係咁嘅：

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,.$

呢兩條式喺 s=0 嘅時候都係無意思嘅，但係佢嘅解析延拓就可以：

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!,$

已知Γ(1) = 1，用以上呢條式再套用極限$s\to 0$就得到

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right)=-{\frac {1}{2}}$

用呢個角度睇，1 + 1 + 1 + 1 + ⋯ = ζ(0) = −1/2。

順帶一提，用同樣嘅方法但係代唔同嘅$s$值入去，可以搵到其他數列嘅和，例如ζ(-1)=1 + 2 + 3 + 4 + ⋯=–1/12，ζ(-2)=1 + 4 + 9 + ... = 0，通式係

$\zeta (-s)=\sum _{n=1}^{\infty }n^{s}=1^{s}+2^{s}+3^{s}+\ldots =-{\frac {B_{s+1}}{s+1}}$

其中B_k係伯努利數。

Emilio Elizalde引述過其他人對呢個級數嘅睇法：

In a short period of less than a year, two distinguished physicists, A. Slavnov and F. Yndurain, gave seminars in Barcelona, about different subjects. It was remarkable that, in both presentations, at some point the speaker addressed the audience with these words: 'As everybody knows, 1 + 1 + 1 + ⋯ = −1/2.' Implying maybe: If you do not know this, it is no use to continue listening.

粵譯：喺短短一年入面，兩個物理學家A. Slavnov同F. Yndurain喺巴塞隆拿講關於唔同課題嘅演講，值得留意嘅係，喺兩個演講入面，講座都提到：「係人都知，1 + 1 + 1 + ⋯ = −1/2，隱含嘅意思可能係，「如果你唔知嘅話，聽落去都無意思啦。」

睇埋

• Grandi級數
• 1 − 2 + 3 − 4 + · · ·
• 1 + 2 + 3 + 4 + · · ·
• 1 + 2 + 4 + 8 + · · ·
• 1 − 2 + 4 − 8 + ⋯
• 1 − 1 + 2 − 6 + 24 − 120 + · · ·
• 調和級數

外部連結

• OEIS sequence A000012 (The simplest sequence of positive numbers: the all 1's sequence)