方差
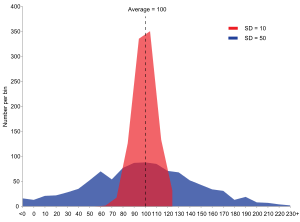
喺概率論同統計學入面,方差(又叫變異數)量度一堆數據分得幾散,即係一組數同佢哋嘅平均數之間爭幾遠,係隨機變數同佢個總體均值或樣本均值嘅離差平方嘅期望值。方差嘅值域係正數,而愈高方差即係話堆數據距離平均數愈遠。
方差喺統計中好重要,用到佢嘅領域包括敘述統計學、推論統計學、假設檢定、度量適合度,同埋蒙地卡羅採樣。由於科學分析時時要用到統計,方差亦都係重要嘅科研工具。方差係標準差嘅平方、分佈嘅二階動差,以及隨機變數同佢自己嘅協方差,佢常用嘅符號表示有、、、,同埋。[1]
攞方差睇數據分得幾散,係因為佢好計過其他離散指標(譬如平均差);譬如,一組唔相關嘅隨機變數和嘅方差等於佢哋方差嘅和。喺實際用嘅時候,方差有個缺點:佢同隨機變數嘅單位唔同,而標準差就單位一樣,所以計完方差之後通常都會開平方用翻標準差嚟計量離散程度。
有兩個唔同嘅概念都叫做「方差」。一種係上便講嘅,係理論概率分佈嘅方差。而另一種方差係一組觀測值嘅特徵。觀測值通常係響真實世界嘅系統中測量嘅。如果計晒成個系統所有可能嘅觀測,用佢哋算出嚟嘅方差叫做總體方差;但係,一般情況下我哋只使用總體嘅一個子集(樣本),用佢哋算出嚟嘅方差叫做樣本方差。攞樣本計算出嚟嘅方差可當成係成個總體嘅方差嘅估計量。
參考
編輯- ↑ Wasserman, Larry (2005). All of Statistics: a concise course in statistical inference. Springer texts in statistics. p. 51. ISBN 9781441923226.




