統計學
統計學(粵拼:tung2 gai3 hok6;英文:statistics)係數學嘅一個子領域[1][2],專門研究點樣喺各個科學領域當中搜集、分析、演繹同埋呈現數據。喺用統計方法嚟研究啲乜嗰陣,個科學家會跟以下噉嘅步驟:首先講明佢研究緊乜嘢變數;跟手就搵個特定嘅總體(指一柞有某啲共通點所以俾人擺埋一齊研究嘅個體)嚟研究;由呢個總體嗰度抽個樣本出嚟[3];喺個樣本度收集數據,睇吓個樣本入面每個個體喺啲變數度嘅數值係幾多[4][5];用某啲統計分析方法嚟去搵出柞變數之間有乜嘢關係[6][7]。
例如有個生物學家想研究吓狼嘅獵食行為同地方嘅氣候之間有冇拏褦。喺呢份研究入面,佢研究緊嘅變數包含咗喺「啲狼嘅獵食行為」(應變數)同「啲狼身處嘅地方嘅氣候」(自變數);佢會將成個世界嘅狼擺埋一齊研究(全世界嘅狼就係研究嘅總體);但世上咁多隻狼,要攞嗮佢哋嚟觀察嘥時間得滯,所以佢就用隨機抽樣-隨機噉由全世界嘅狼嗰度抽(例如)100 隻出嚟研究;跟住佢就要向個樣本收集數據,用各種嘅方法去量度樣本入面每一隻狼(一隻狼為止一個個體)嘅獵食行為-好似係隻狼每日用幾多個鐘頭獵食、食咗幾多公斤嘅肉呀噉-同埋佢身處地方嘅氣候-好似係嗰個地區落雨落得有幾密同平均氣溫等等;攞完數據之後,研究者就要用各種統計分析嚟計吓柞變數之間有乜拏褦。
同樣嘅做法喺物理科學同社會科學嗰度都會用到[1]。因為統計學廣泛嘅應用價值,統計學知識經已成為咗現代科學研究上走唔甩嘅一個部份,大學科學學科嘅本科課程基本上冚唪唥都會教統計學嘅嘢[8][9]。
背景
編輯科學方法
編輯科學哲學[e 1]係科學嘅基礎,簡單講就係指科學家對於「科學係乜同埋應該點搞」嘅睇法。科學哲學嘅基礎係科學方法,意思係話科學研究係用以下嘅步驟嚟理解宇宙當中可觀察嘅事物,嘗試預測未來嘅現象[10][11]:
- 根據手上已知係真嘅事實,諗一啲理論出嚟-「基於我哋經已觀察到嘅呢啲現象,我推測啲現象背後嘅物理法則係噉噉噉,令物質能量有呢啲行為」,呢啲理論最理想係用數學模型嘅方式表達嘅;
- 跟手就靠邏輯嘅思考,去諗吓呢柞理論會做點樣嘅預測-「如果我提倡嘅呢個理論係真確嘅,理應會...」;
- 然後就做實驗同觀察嚟攞數據,驗證吓個理論嘅預測係咪真確-「如果我呢個理論係真確,呢個實驗理應會得出某個某個結果,而個實際嘅實驗結果係...」;
- 如果數據顯示,個理論係做唔到準確嘅預測嘅話,就要一係根據攞到嘅數據睇吓個理論要點改先可以令佢做到準確啲嘅預測,一係就要諗新理論取代舊理論[12]。
上述嘅過程會係噉重複,直至手上嘅理論做到完全準確嘅預測為止-於是科學就有持續嘅發展,做到愈嚟愈準嘅預測。到咗現代,科學上經已有龐大嘅理論體系,按所研究嘅現象分做物理學(用科學方法研究宇宙基本定律)、生物學(用科學方法研究生命)、心理學(用科學方法研究人嘅行為)同社會科學(用科學方法研究社會)等嘅多個領域,每個領域都有諗出用嚟描述同預測自己所研究嘅現象嘅理論,而一啲重要嘅理論(例如係進化論)往往俾科學家用實驗同觀察驗證過上百次-非常經得起考驗,所以學界一般認為呢啲理論係有返咁上下正確嘅模型[e 2]-能夠充分噉描述現實。除此之外,科學家仲會不斷搵新嘅現象研究,睇吓呢啲理論能唔能夠解釋新現象,又或者使唔使諗新嘅理論,令科學知識得以持續噉發展[13][14]。
推論問題
編輯歸納[e 3]係科學家嘅基本諗嘢方法,指由啲個別嘅事例嗰度去推斷出一啲普遍原理。响歸納性質嘅論證入面,前提真確冇辦法保證到結論真確,只係可以靠住大量嘅事例嚟提升個論證嘅強度,好似係以下呢個論證噉[15]:
- 前提:我之前見過嘅天鵝都係白色嘅:
- 結論:呢個世界上所有天鵝都係白色嘅。
呢個係一個典型嘅歸納論證:就算個前提係真,都保證唔到個結論係真-前提入面嗰個「我」並冇見過嗮世界上所有嘅天鵝,而事實係世界上有黑天鵝,個觀察者會噉諗只不過係因為佢咁啱未見過黑天鵝;如果個觀察者想佢個論證強啲嘅話,佢就一啲要去見多啲天鵝:如果佢睇勻嗮全歐洲嘅天鵝,呢個論證嘅說服力會比較強;相反,如果佢淨係見過英國嘅天鵝,噉呢個論證嘅說服力會渣好多。科學家都係跟住呢種諗嘢方式搞科學:喺驗證「萬有引力係真嘅」呢句說話嗰陣,牛頓觀察到一個蘋果由樹上面跌落嚟,佢亦都觀察到好多嘢都係跟呢條規則,但佢始終冇辦法去真係「證明」呢個宇宙入面真係所有嘢都有萬有引力-因為可能喺宇宙嘅某啲黑暗角落度會有啲冇引力嘅嘢,只係人類仲未搵到。科學家靠嘅係實驗同觀察,佢哋冇辦法好似數學家噉真係證明佢哋講嘅嘢,只可以靠住重複做實驗同觀察嚟加強自己嘅論證,但始終係冇方法排除一個可能性:呢個宇宙入面可能真係有啲嘢係唔跟佢哋諗出嚟嗰啲定律嘅,只係佢哋未搵到呢啲嘢[16]。
就係因為噉,喺正式嘅科學論文入面,科學家好少可會話自己「證明」咗乜嘢乜嘢理論,只係會話「觀察同實驗嘅證據結果撐嗰個理論」,而且佢哋仲會好積極噉去搵新數據,睇吓呢啲佢哋之前未見過嘅數據會唔會推翻舊嘅理論。如果會嘅話,佢哋就會開始諗新理論,或者睇吓點樣將舊嗰個理論改吓等個理論可以同新數據夾得埋[17]。
定位
編輯喺定義上,統計學就係為咗思考「點樣由手上數據推導出普遍知識」而生嘅數學子領域[18],尤其關注帶有不確定嘅數據[19]:無論係邊個科學領域,科學家做嘅都係「由手上睇到嘅現象(樣本嘅數據)嗰度嘗試推導出能夠廣泛噉描述同類現嘅理論」,呢種做法本質上就有不確定-難以保證個樣本實係代表到個總體,例如研究者想研究狼嘅體重,因為人力物力嘅限制,佢冇可能研究嗮古往今來所有嘅狼,所以佢就去搵 100 隻狼(樣本)返嚟做研究,佢量度到呢個樣本嘅狼平均體重係 40 kg(數據),就最嚴格嘅邏輯基準嚟講,呢個數可能
- 真係代表到全世界嘅狼;但又有可能
- 全世界嘅狼嘅平均體重查實係 60 kg,個研究者之所以搵到 40 kg 呢個數只係佢咁啱得咁橋唔好彩,抽到個代表唔到個總體嘅樣本;
喺呢個思考過程當中,就經已必然涉及「手上嘅樣本有幾大機會代表到全世界嘅狼」嘅問題,會用到機會率[e 4]同埋相關嘅數學概念(可以睇埋概率論)。好似機會率等科研工作上用嚟分析數據嘅數學概念就形成咗統計學呢門學問[20]。
統計學用途好廣泛。喺科學上,數據係好重要嘅一環,噉係因為科學嘅基礎係實證。科學家嘅職責係諗啲理論出嚟解釋自然現象,而佢哋發表親啲乜嘢理論都一定要搵證據嚟驗證吓個理論。要驗證一個理論就要去現實世界嗰度收集數據-所以搞科研實會有一大柞數據要處理[21][22]。除此之外,統計學喺商業範疇上都有用:統計師會喺一啲公司嗰度幫手解答一啲研發上遇到嘅問題[23]。
兩大範疇
編輯統計學大致上分做兩範,負責總括同埋形容啲數據嘅叫敘述統計學[e 5],而用一啲分析方法嚟去估計同研究變數與變數之間嘅關係嘅就叫做推斷統計學[e 6]。前者會俾出一啲好似啲變數嘅平均值等嘅資訊,而後者會將數據入面嘅資訊變做數學模型,而呢啲數學模型打後可以用嚟做出預測,例如分析幾個變數之間嘅關係有幾勁[24]。
攞返上面個狼研究嘅例子做說明,假設做完推斷統計分析之後,發覺一隻狼每日食嘅嘢嘅總量(以 kg 嚟計)同佢身處嘅地區嘅平均氣溫(以攝氏計)成反比(即係一隻狼身處嘅地方愈凍,佢就愈食得多嘢),而佢哋之間嘅關係可以大致上用一條式表達(可以睇吓迴歸分析):
- ,設 做「隻狼食幾多 kg 嘢食」而 做「佢身處嗰度嘅平均攝氏氣溫」, 同 係某啲實數。
收集咗一輪數據之後,就有得用啲數據嚟估計 同 嘅數值,打後下次再搵到隻狼嗰陣就可以用呢個模型嚟按佢身處嗰度嘅平均氣溫嚟估計佢每日會食幾多嘢。一般嚟講,收集到嘅數據愈多(喺呢個例子入面即係研究過愈多嘅狼),可以做到嘅預測就會愈準[25]。
收集數據
編輯收集數據[e 7]係做統計分析必要嘅一個工序:用科學方法做研究係要由對現實嘅觀察當中歸納出一啲能夠描述現實嘅法則或者理論;而要對現實作出系統化嘅觀察,就一定要攞數據-用某啲符號(喺統計學上通常係數目字)記低現實世界嘅狀態[26]。
變數
編輯變數[e 8],又叫做「未知數」,係做統計學一定會處理嘅嘢。變數指喺宇宙入面一啲有可能變、兼且係形容緊某啲事物嘅特性。例如身高、體重同宗教呢啲特性都可以用嚟形容人,而且呢幾樣嘢個個人唔同,所以呢三個都係屬於「用嚟形容人」嘅變數。大細同質量呢啲可以攞嚟形容人或者物件都得,而且呢兩樣嘢個個人或者件件物件都可以唔同,所以係屬於「形容人同物件」嘅變數[27]。
變數大致上有得分做兩種:
- 連續變數[e 9]指啲有得用數字嚟量度、兼且去到小數點後幾多位都得嘅變數,呢啲數值攞得嚟比較大細同埋做數學嘅運算,例如人有幾高有幾重都可以講係連續變數-身高同體重有得用數字嚟度,兼且可以用有小數點嘅數字,而人有得用呢柞數值嚟比較唔同人嘅身高同體重,仲可以用佢哋嚟計數;
- 相反,好似屬邊個宗教呢個社會科學上成日研究嘅變數就係一個唔連續變數[e 10]-宗教唔可以用數字嚟度,而佢嘅值一般都唔可以攞嚟計數-好似係 183 厘米同 80 公斤呢啲數值有得加減乘除,而信佛同信耶穌呢啲值雖然都係形容緊啲嘢,但唔可攞計數機去撳加減乘除。連續變數喺統計學入面比較常見-因為前者先至可以攞嚟計數,而後者唔得[28]。
變數可以話係科學嘅關鍵,因為無論係邊個學科,科學嘅重點基本上就係想搵出變數同變數之間有啲乜嘢關係,而「知道嗮成個宇宙入面所有嘅變數同埋佢哋之間嘅相互關係」基本上就係科學嘅終極目標。
抽樣
編輯抽樣[e 11]係做科研嘅一個程序,指由個總體嗰度攞一部份嘅個體嚟研究。所有研究都係研究緊某啲總體[e 12],例如喺上面個狼例子個總體就係「世界上嘅狼」,而(例如)心理學所研究嘅總體就係「世界上所有嘅智人[e 13]」。但研究嘅總體通常都太大,搞到研究佢哋嘅科學家好難由個總體入面嘅所有個體收集數據,例如世界上有數以億計嘅人,要逐個逐個噉嚟研究太嘥時間,根本冇可能行得通,於是乎科學家喺做研究嗰陣往往要做抽樣-由研究緊個總體嗰度抽一小部份出嚟,而呢個部份就係所謂嘅樣本[e 14],希望透過研究呢一小部份嚟去了解嗮總體入面所有嘅個體。例如係想研究黑洞嘅話,天體物理學家可以去搵 10 個特定嘅黑洞嚟研究,希望透過研究呢 10 個黑洞(呢 10 個黑洞只係全宇宙成千上萬個黑洞之中嘅一小部份)嚟了解埋其餘嘅黑洞[29]。
抽樣呢個程序係做科研好關鍵嘅一環,因為做抽樣嗰個科學家一定要確保到佢抽出嚟個樣本真係代表得到成個總體,噉先至可以說服到啲人話佢個研究得出嘅結果可以普遍化[e 15]到去成個總體嗰度。例如係頭先嗰個狼研究噉,一個動物學家有至少兩個抽樣方法可以揀:
一般認為,後者更加代表得到嗮個總體-「全世界嘅狼」-而前者就比較有以偏概全之嫌。好多時啲科學家詏話一份研究冇辦法將得出嘅結果普遍化,都係指控緊佢個樣本唔夠代表性,好似係好多廿世紀嘅心理學家喺做心理學研究嗰陣都貪方便,喺大學度攞啲大學生嚟做研究嘅樣本,搞到科學界成日都話佢哋嗰啲所謂嘅心理學只不過係「大學生嘅心理學」,根本代表唔到大學生以外嘅群體嘅心理[30]。
量度
編輯要做統計,就實要首先將啲現實世界入面嘅變數轉化做數據入面嘅數字,呢個過程就係所謂嘅量度,攞個磅重磅磅一隻動物嘅過程係量度緊隻動物嘅重量(將「隻動物嘅重量」呢個變數轉化做一個數字),而做智商測驗[e 16]嘅過程就係量度緊一個人嘅智能(將「個人嘅智能」呢個變數轉化做一個數字)... 呀噉。而量度層次[e 17]係統計學上嘅一個概念,係指基於一個量度方法提供到幾多資訊嚟到劃分嘅分類法,可以話係反映一個量度方法有幾「好使」,一共有四層[31][32]:
| 層次 | 名 | 用得嘅邏輯同數學運算 | 例子 | 點計中間趨勢 | 點計離散趨勢 | 定性抑或 定量 |
|---|---|---|---|---|---|---|
| 名目 [e 18] |
、 | 二元名目:性別(男、女)、真實性(真、假)、出席狀況(出席、缺席) 多元名目:語言(廣東話、普通話同英文等)... |
眾數 | 冇 | ||
| 次序 [e 19] |
、 ; 、 | 多元次序:服務評等(傑出、好、欠佳)、教育程度(小學、初中、高中、學士、碩士同博士等) | 眾數、中位數 | 分位數 | ||
| 等距 [e 20] |
、 ; 、 、 |
溫度、年份、緯度等 | 眾數、中位數、平均數 | 分位數、全距 | ||
| 等比 [e 21] |
、 ; 、 、 ; 、 |
價錢、年齡、身高、絕對溫度、絕大多數嘅物理量 | 眾數、中位數、平均數等 | 分位數、全距、標準差等 |
一般嚟講,科學家都想自己嘅研究嘅量度層次盡可能有咁高得咁高(即係盡可能接近等比),不過現實世界嘅技術等嘅限制唔一定俾到佢哋噉樣做。
順帶一提,除咗層次之外,科學家亦都好關注量度方法嘅信度[e 22]同效度[e 23]:信度同效度係兩種用嚟衡量一種量度方法掂唔掂嘅基準;信度指用嗰個方法對一樣嘅現象進行重複觀察之後係咪可以得到相同嘅結果,而效度係指個方法有幾量度到佢理應要量度嗰樣嘢,喺心理測量學(研究用統計方法量度心理特性嘅領域)等嘅領域上,研究者仲會有多種方法評估一種量度方法嘅信度同效度[33][34]。
敘述數據
編輯喺搵咗數據返嚟之後,研究者手上會有個數據集[e 24],每個個案都會喺每個變數上有個數值,而一般嚟講,研究者首先會做嘅係搵一啲指標描述吓柞數據大致係點樣嘅(敘述統計學),常用嘅敘述統計指標包括咗[35]:
- 平均數[e 25]:平均數( )最常係指將啲個案嘅數值( )加埋一齊,再除以個案數量( ):
- 變異數[e 26]( ):以下嘅數值:
- ,
- 當中 係個案數量, 係第 個個案喺個變數上嘅值,而 係個樣本嘅平均值- 反映咗啲個案平均距離平均值幾遠。
- 標準差[e 27]( ):變異數嘅開方。
... 等等。
概率分佈
編輯概率分佈[e 28]係成日用嚟描述「柞數據乜嘢樣」嘅架生。一個概率分佈係一個數學函數[e 29],而呢個函數表達咗每個數值喺某個總體或者樣本入面出現嘅概率(機會率), ,當中 就係個概率分佈。例如假設而家掟一個銀仔,用 代表掟個銀仔嘅結果,掟 10 次(個總體係「全世界嘅掟銀仔結果」,而呢 10 次就係一個樣本)。 係公嘅機會率係 0.5(即係 50%),而 係字嘅機會率都係 0.5(假設個銀仔冇做過手腳),相應嘅概率分佈如下[36][註 1]:
- 公 ,「 係公嘅機會率係 50%」。
- 字 ,「 係字嘅機會率係 50%」。
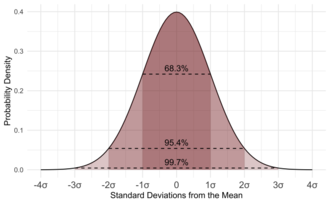
响現實世界嘅科研入面,啲變數好少可會「一係公一係字」咁二元,但個原理一樣:常態分佈[e 30]就係科學入面最常用嘅概率分佈之一,如果由一個常態分佈嘅總體嗰度抽樣,個變數嘅平均值會係出現得最密嘅數值,低過平均嘅數值同高過平均嘅數值出現嘅機會率一樣,而離平均值愈遠嘅數值,抽到出嚟嘅機會率就愈低,如果按住個樣本畫一個概率分佈圖(打橫個條 X 軸係個變數嘅可能數值,而打戙嗰條 Y 軸係每個數值出現嘅機會率),一個常態分佈會俾出一條好似鐘噉嘅形狀嘅線[e 31]。常態分佈嘅概率密度函數係( 係個分佈嘅標準差)[37]:
譬如話以下呢個情況噉:想像有生物學家想研究成年中華白海豚嘅身長,但佢冇可能捉嗮世界上咁多隻白海豚遂隻遂隻嚟度佢哋幾長,於是乎佢就抽個樣本出嚟,用個樣本嚟估計全世界嘅白海豚嘅身長;呢個樣本入面有 20 隻白海豚,佢哋嘅平均身長係 2.2 米,唔係隻隻都啱啱好 2.2 米長-有隻係 1.8 米長,有隻係 2.6 米長呀噉-但一隻白海豚身長高過呢個值嘅機會率大致上等如佢身長低過呢個值嘅機會率,而且離 2.2 米愈遠嘅數值出現嘅機會率愈低。如果畫幅概率分佈圖,「隻白海豚嘅身長」做 X 軸,而「每個身長數值出現嘅機會率」做 Y 軸,幅圖會出一條近似鐘形嘅線。
一般嚟講,做統計嗰陣都會假設抽樣個過程係獨立同分佈[e 32]嘅-噉講嘅意思係指,樣本入面每個個體嘅數值喺由個總體嗰度抽出嚟嗰陣嘅概率分佈都係一樣,而且相互之間獨立[e 33](一個抽到嘅數值嘅概率分佈唔會影響到下一個抽到嘅數值嘅)。呢個假設慳咗好多時間同精神-如果吓吓做統計都要諗第二個抽出嚟嘅數值同第一個抽出嚟嘅數值嘅概率分佈會唔會唔同咗嘅話,計起統計上嚟就會撈絞得好交關[38]。
相關定實驗性質
編輯得到咗呢啲數值之後,研究者就可以做進一步嘅分析,理解變數之間嘅關係,而研究有得大致上分做兩種:相關性質[e 34]同實驗性質[e 35][39]:
相關性質
編輯相關研究嘅目的係要搵出變數之間嘅統計相關[e 36]有幾勁。皮亞遜積差相關係數[e 37]係統計學成日用嘅一個指標,「兩個變數 同 之間嘅皮亞遜積差相關係數」( )係噉樣定義嘅:
呢條式會得出一個相關值,個數值會喺 -1 同 1 之間,負數表示兩個變數成反比(一個數值高嗰陣另一個傾向數值低),而正數就表示兩個變數成正比(兩個數值傾向一齊高或者一齊低),個相關值愈接近零表示兩個變數之間嘅關係愈弱,而如果個相關值等於零就表示兩個變數根本唔啦更。喺做相關性研究嗰陣科學家會先收集一啲數據,再用好似上面呢條式等嘅方法計出變數之間嘅相關值,搵出研究緊嘅變數之間有乜嘢啦掕,而呢個過程俾出嚟嘅資訊喺將來有得攞嚟預測某啲現象[40]。
實驗性質
編輯實驗性研究可以話係做得再犀利啲,仲可以幫手搵出變數之間嘅因果[e 38]關係。齋靠觀察變數之間嘅統計相關做唔到搵出事物之間嘅因果關係,噉係就算一個研究者觀察到 同 之間有顯著嘅正統計相關,噉依然有三個可能性:
上述嘅就係所謂嘅相關唔蘊含因果[e 39]問題-就算一個研究者搵到兩樣嘢之間有統計相關,都唔能夠即刻判斷兩樣嘢之間嘅因果關係。一般認為喺科學上,要搵出事物之間嘅因果關係,就實要靠實驗嘅方法:實驗係指研究者特登操作[e 40]某啲變數,再睇吓個操作會造成乜嘢效果,例如「如果佢特登操作 ,就會見到 跟住出現,而如果佢唔特登操作 , 就唔會跟住出現」,佢就有理由相信 真係能夠引致 。順帶一提,因為廿世紀嘅社會科學好多時都係齋靠觀察嘅相關研究,所以成日俾人插佢哋,話佢哋唔能夠確立唔同社會現象之間嘅因果關係[42][43]。
一個實驗嘅基本步驟係噉嘅[42]:
- 响做實驗之前,要用過往嘅文獻同理論嚟諗吓研究緊嘅變數之間會有啲乜嘢因果關係;
- 將研究嘅對象擺喺一個受控制嘅環境[e 41]裏面-「受控制嘅環境」指一個受人工控制,唔會俾啲外來因素干擾嘅環境,例如係一間實驗室;
- 將研究嘅對象分做至少兩組-實驗組[e 42]同對照組[e 43];
- 喺實驗組嗰度人工噉操控「因」(呢個係自變數;IV)嘅變數嘅數值,而對照組就唔郁;
- 比較吓兩個組別喺「果」(呢個係應變數;DV)個數值係點;
- 如果實驗組喺應變數嘅平均值上同對照組顯著噉有差異(可以睇埋學生 t 測試),噉就可以話發現咗一個因果關係-自變數嘅變化會令到應變數跟住起變化。
有經濟學同管理學方面嘅學者試過喺美國伊利諾伊州嘅一間工廠嗰度過所謂嘅霍桑效應[e 44]實驗。喺呢個實驗當中,啲研究者想研究俾人睇住會點樣影響工人嘅生產效率-佢哋研究嘅總體係世界上所有嘅工人,但佢哋冇可能一次研究嗮咁多工人,所以只係攞咗一小部份嚟研究-嗰間工廠嘅工人(抽樣)。佢哋跟住做以下嘅嘢:
- 佢哋嘗試增強間廠入面嘅燈光(燈光係 IV),而燈光影響啲工人會唔會俾人睇到(IV 理應會引致嘅嘢),睇吓佢點樣影響流水線工人嘅生產率(生產率係應變數);
- 研究人員首先檢測咗間廠既有嘅生產率,打後再改變車間嘅燈光強度(人工噉操控 IV 嘅數值),再睇吓有乜嘢結果;
- 結果係生產率喺實驗環境之下提升咗-表示「燈光」同「生產率」兩個變數之間有關係,而且前者係因,後者係果。
呢個實驗好出名,不過有唔少科學家都嫌呢個實驗嘅設計有少少唔掂,例如係缺少咗對照組同埋「實驗環境唔係咁受控」呀噉[44]。
假說檢定
編輯假說檢定[e 45]可以話係推論統計學當中最重要嘅一個工序,指驗證一個假說(指一個仲未搵到證據支撐,但研究者有理由認為好可能係真確嘅論述)嘅過程。一個做假說檢定嘅研究者所做嘅工序如下:
- 睇過有關佢所研究嗰樣嘢嘅文獻,
- 建基於已有嘅知識,作出一啲有關嗰樣嘢嘅新假說—「我睇過打前嘅研究,我認為有咗已知嘅嘢,我可以作出以下嘅判斷,而驗證呢個判斷係咪正確能夠帶嚟新知識」,
- 諗出一個驗證呢假說嘅程序,
- 用呢個程序攞數據,
- 對數據作出分析,
- 用分析結果判斷個假說係咪真確[45]。
假說檢定嘅過程會用到以下嘅概念:
估計量
編輯嚴格嚟講,個總體嘅參數[e 46](指形容緊某個系統嘅特性)係不可知嘅-淨係有得透過個樣本嘅數值嚟估吓呢啲參數嘅數值。例如喺上面個中華白海豚研究嘅例子噉,要知道嗮古往今來所有中華白海豚嘅身長原則上係冇可能嘅,所以研究者亦都冇方法知道「全世界嘅白海豚嘅平均身長」嘅真正數值-唔單只啲科學家唔夠人力物力度嗮世上咁多隻白海豚,而且過去嘅白海豚同埋仲未出世嘅白海豚嘅身長都係冇辦法量度嘅,所以成個研究啲科學家都係喺度假設緊個樣本能夠代表到全世界嘅白海豚,並且用個樣本入面嘅白海豚嘅平均身長嚟估計全世界嘅白海豚嘅平均身長。除咗平均值,個樣本嘅變異數等嘅敘述統計資料都會俾科學家攞嚟估計個總體嘅參數,呢啲俾人用嚟估計總體參數嘅就係所謂嘅估計量[e 47][46]。
信心區間
編輯做科研嗰陣啲研究人員可以睇到嘅就淨係得個樣本嗰啲數值,而個總體嗰柞真實嘅數值係不可知嘅,所以任何由個樣本嗰度估計出嚟嘅數值頂嗮櫳都淨係有得話係個總體嘅近似值。信心區間[e 48]係指「有信心總體個真實數值係喺入面嘅區間」,喺做統計嗰時會俾人攞嚟表述個樣本嘅數值同個總體嘅真實數值之間估計差幾遠,
舉個例說明,最常用嘅係「95% 信心區間」( ),用返上面白海豚嘅例子,啲科研人員會用個樣本入面嘅海豚嘅身長平均值嚟估計嗰個不可知嘅「世上所有白海豚嘅身長嘅平均值」( ),而佢哋可以用一啲統計方法計個「白海豚身長平均值嘅 95% 信心區間」出嚟-呢個值係指「有信心 95% 機會世上所有白海豚嘅身長嘅平均值嘅真實數值係喺 同 之間」[47]。
虛無同備擇假說
編輯虛無假說[e 49](符號: )同備擇假說[e 50](符號: )係做科研上成日會用到嘅行話:
- 虛無假說係指做一份研究嗰陣嘅預設立場,指「兩個量度嘅變數之間冇關係」呢句嘢,而
- 備擇假說係做一份研究嗰陣嘗試驗證嘅立場,指「兩個量度嘅變數之間有關係」呢句嘢。
舉個例說明,假想有個認知心理學家想驗證「年紀」同「記憶力」呢兩個變數之間嘅關係,於是佢就搵咗兩批人返嚟做佢嘅樣本,第一批人年紀喺 20 至 30 歲之間,第二批人年紀喺 50 至 60 歲之間,再用一啲測試量度呢兩批人嘅記憶力,設第一批人喺記憶力測試上嘅平均得分係 ,而第二批人喺同一柞測試上嘅平均得分係 ,噉呢份研究嘅 係 , 係 ,當中後者係個認知科學家想證實嘅嘢[48]。虛無假說同備擇假說呢兩個詞語查實好簡單,但呢兩個詞語令到寫科研報告嗰陣慳好多位-啲科學家唔使吓吓都講嗮成句假說出嚟[49]。
喺做假說檢定嗰陣,一般會將可能會出現嘅錯誤分兩種[50]:
- 第一型錯誤[e 51]指錯誤噉否定咗 ,得出咗個假陽性[e 52]結果-兩個變數查實有啦掕,研究者但搵到咗一個陽性結果出嚟。
- 第二型錯誤[e 53]指 其實係錯,但就冇俾人成功噉否定到,得出咗個假陰性[e 54]-兩個變數實際上有關但就搵到個陰性結果。
呢啲錯誤會發生有好多原因,包括係科研入面嘅某啲隨機性-例如有份研究想睇吓兩個地區嘅狼嘅平均身長係咪有分別,佢哋隨機噉喺兩個地區度抽樣,再度吓啲狼嘅身長,可能兩個地區啲狼嘅平均身長係冇分別嘅( 係真),但喺隨機抽樣嘅過程當中,咁啱得咁橋喺地區 抽咗啲嗰頭最大隻嘅狼出嚟,而喺地區 又咁橋淨係抽嗮啲嗰頭最細隻嘅狼出嚟,搞到最後搵到出嚟個結果話兩個地區啲狼嘅身長有顯著分別,即係錯誤噉排除咗 -第一型錯誤。喺呢個個案入面,啲科研人員之所以搵到兩個變數(地區同埋啲狼嘅身長)之間有關唔係因為兩者之間真係有關,而係抽樣嗰陣唔好彩。呢啲事喺科學界間唔鐘會發生[51]。
顯著性
編輯統計顯著性[e 55](符號係 )[52],簡稱顯著性,反映一個俾統計者接受咗嘅假說
- 「有幾大機會係真確。」
事實上,統計學喺答問題嗰陣好少可會話俾到真同假咁二元嘅答案。統計方法本質上係帶咗些少隨機性喺度,好似係頭先提咗嘅第一型錯誤嘅例子就顯示到,無論一份研究點精密,都梗會有少少機會會出錯,而呢啲錯誤好多時係人為冇可能控制得到嘅:啲科學家一方面冇可能度得嗮古往今來所有嘅狼嘅身長,但另一方面,佢哋一做抽樣,就梗會有機會攞到個代表唔到個總體嘅樣本-即係話無論點,用統計方法硬係會或多或少帶有啲不確定。於是乎統計學家就決定咗:用統計學做親啲乜嘢研究嗰陣,都唔會俾二元性嘅答案,而係會俾出好似信心區間呢類「某句嘢有幾大機會係啱」呢類帶咗啲機會率喺度嘅答案,而 就係用嚟做呢樣嘢嘅概念[53]。
- 睇到個噉嘅結果 係真 [註 2]
一般嚟講,如果柞統計分析顯示 嘅數值係細過某個特定嘅數值(通常係 5%)嘅話( )[註 3]-「如果 係真,會得出呢個結果嘅機會好微」,噉研究者就有夠強嘅理由相信 好有可能唔係真,噉做分析嗰個人就會當句 係真確嘅,並且拒絕個虛無假說[e 56]。喺實際嘅科研論文當中做統計嘅話,研究者幾乎實會報告自己做咗統計分析得出嘅 值,並且用「 值好細」呢一點嚟說服人,話自己嗰句 係真嘅[45]。
比較平均值
編輯要測試一個 ,其中一種最常見嘅做法就係比較平均值[e 57],即係比較個樣本入面唔同組之間喺個變數嘅平均值上有冇差異。喺最簡單嗰種情況-得兩組要比較-之下,研究者可以用學生 t 測試[e 58](以下簡稱 t 測試)。學生 t 測試呢種方法可以攞嚟分析兩個組(通常係實驗組同對照組)之間喺個指定變數嘅數值上係咪有顯著嘅差異,當中最原始嗰種獨立樣本 t 測試[e 59]係 t 測試嘅一種,獨立樣本 t 測試假設咗三點[54]:
用返同上面類似嘅例子,班研究人員可能想做個實驗,睇吓提高氣溫會唔會改變狼嘅食量,佢哋可以
- 隨機噉由全世界嘅狼嗰度抽一柞(例如係 200 隻)出嚟,將佢哋分做兩組-實驗組同對照組,兩組各有 100 隻狼,將前者擺喺一個有暖氣嘅環境度養,而後者就擺喺一棟模仿自然環境(氣溫正常)嘅地方度養(氣溫係自變數);
- 跟手啲研究人員就要量度個應變數(食量)-一個可能嘅方法係用攝影機監察住啲狼嘅一舉一動,佢哋一食嘢就記錄低,並且用影片影到嘅影像估計樣本入面嘅每隻狼大約每日食咗幾多公斤嘅嘢食。呢個步驟會得出一大柞數據,表述每一個個體喺個應變數上嘅數值(即係每隻狼嘅日常食量),而
- 由呢啲數據嗰度,研究者亦會順理成章噉計到兩個組分別喺個應變數上嘅平均值-「實驗組啲狼嘅平均日常食量」( )同「對照組啲狼嘅平均日常食量」( );
- 下一步就要睇吓 同 之間係咪有顯著嘅分別-如果有,研究人員就有得否定個 ,並且話今次攞到嘅實驗數據撐佢哋個 ( 係「提高氣溫會影響狼嘅食量」呢句嘢)。
- 因為佢哋嗰兩個組入面個體係分別噉抽樣嘅,而且得一個應變數(狼嘅食量),所以佢哋可以用獨立樣本 t 測試。
用好似 t 測試噉嘅統計分析可以提高一份研究嘅說服力:一方面,啲研究者可以淨係靠直接比較兩個組喺個變數上各自嘅平均值( 同 ),但噉做唔會有乜嘢說服力;個變數係大致上呈常態分佈嘅-一隻狼嘅日常食量通常會接近所有狼嘅日常食量嘅平均值,離平均值愈遠嘅數值就會出現得愈少;如果齋靠比較兩個組嘅平均值,就等於冇考慮到抽樣等過程入面嘅隨機性-可能只係抽樣嗰陣唔好彩,大食嘅狼咁橋分嗮去實驗組嗰度,而食嘢少嘅狼就咁啱分嗮去對照組。於是啲研究人員為咗要提高佢哋份研究嘅說服力,就要攞啲數據嚟計吓[55]。
t 測試流程
編輯要評估兩組之間嘅差異嘅顯著性,首先要計兩組嘅標準差(符號係「 」或者「 」)出嚟:
- ,當中
係樣本大細(個樣本入面嘅個體數量,樣本嘅嘥
係成個樣本嘅大細,而 同 就係兩個組分別喺個變數上嘅平均值, 係兩個組嘅標準差(假設咗兩個組嘅標準差相等),最後計到一個 值出嚟,呢個數值同「兩個組嘅平均值嘅差距」成正比,同「兩個組嘅標準差」成反比。如果 值好大,噉就表示咗「兩個組之間嘅差異」大過「組嘅內部差異」好多,噉就表示「個實驗嘅操作造成嘅差異」大過「隨機性嘅個體差異」- 值愈大愈表示個實驗嘅操作嘅效果明顯過個體差異,愈係表示兩個組之間嘅差異係因為實驗嘅操作造成嘅。所以 值愈大, 值( 睇到個噉嘅結果 係真 )理應會愈細[註 4][55]。
t 測試變種
編輯- 配對樣本 t 測試[e 60]:指做 t 測試嗰兩個組唔係獨立同分佈嘅,研究者做咗某啲嘢,令一組數值當中每一個都喺另外嗰組當中有個對應,例如做個心理學實驗,研究者想知個實驗操作會引致變數 有乜變化,於是就喺實驗前量度 一次,跟住對受試者做實驗操作,然後喺實驗後又量度 一次(睇返重複量數設計)。喺呢個情況下,每位受試者都有一個
- 「實驗前嘅 值」( )同
- 「實驗後嘅 值」( ),
- 研究者想比較兩組數值(總共有 個數值,而受試者數量係 ),但兩組數值唔係獨立同分佈嘅-每個 值都有一個相應嘅 值(一位受試者嘅 值同佢嘅 值)[55]。
- 變異數分析[e 61]:一系列用嚟分析唔同組嘅平均值嘅方法;假想家陣個研究者想比較三組喺變數 嘅平均值上嘅差異,如果三組之間有顯著嘅差異,噉組之間嘅 嘅變異數應該會大過組內部嘅好多。最簡單嘅單因子變異數分析[e 62]分析一個應變數喺三個或者以上嘅組之間嘅差異(組就係自變數),考慮以下嘅數值[57]:
- 原則上, 數值愈大,研究者就愈有理由相信組之間有顯著嘅差異。
...等等。
誤用
編輯統計學上嘅數據同分析方法對科研有巨大嘅幫助,但又時不時會俾人誤用。有人就曾經噉講[58]:
| 「 | 粵文翻譯:世上有三種大話:大話、抵死嘅大話、同埋統計數字。
|
」 |
舉附圖嚟說明,同一樣嘅統計數據可以用唔同嘅方法呈現,而唔同嘅呈現方法可以攞嚟誤導人,好似係附圖嗰兩幅棒形圖噉,兩幅圖表達嘅數據一樣,都係表達緊一間公司喺 2010 同 2011 年嘅銷售量(Y 軸係銷售量,X 軸係年份),但係兩幅圖嘅原點唔同-左圖嘅 Y 軸係以 36 做起點,右圖嘅以 0 做起點,令到前者望落好似賺多咗好多錢噉[1]。除此之外,對分析嘅結果又有得用唔同嘅方法解讀,搞到好多人會特登用對自己有利嘅呈現同解讀方法嚟誤導人,而美國作家達利哈夫[e 63]嘅書《How to lie with statistics》(粵文:點樣用統計學講大話)就揭露咗好多生意人同政治家等嘅人物用類似嘅詭計嚟呃人嘅例子[59]。
要預防統計學嘅誤用有好多方法,包括要用啱嘅圖表等等[60]。而且喺將用統計得出嘅結論普遍化嗰陣,要留意佢會唔會超出咗個樣本代表到嘅範圍,只有個當樣本可以代表到個總體嗰陣,統計方法得出嘅結果先至算係可信、精確嘅,例如係一份用白人做樣本嘅醫學研究得出嘅結論未必啱唐人用[61]。
簡史
編輯統計學呢門學問最少有得追溯到去公元前 5 世紀咁久遠。一般認為,最早可以算得上係統計嘅著作嚟自公元 9 世紀嘅《密碼破譯》[e 64]呢本書,由一位阿拉伯人學者編寫嘅。喺呢本書入面,作者佢詳細噉記錄咗點樣用統計數據同頻率分析破解密碼,而學界嘅主流意見認同,統計學同密碼學(研究點樣喺敵人存在下安全通訊嘅學問)就係噉一齊誕生[62][63]。
世上第一本統計學入門書一般認為係源自 14 至 17 世紀。喺 14 世紀,佛羅倫斯嘅銀行家兼執政官佐凡尼·維蘭尼[e 65]編訂咗《Nuova Cronica》呢本歷史書,包括咗好似係人口、法令、商貿、教育同埋宗教場所呢啲嘢在內嘅統計數據,俾人話係歷史上第一本教人做基本統計嘅書;另一方面,有啲學者就將 1663 年莊·葛蘭特[e 66]根據死亡率統計表編訂出版嘅《Natural and Political Observations》(粵文:自然與政治觀察)呢本書定格做統計學嘅始祖[64]。
統計學嘅名可以追溯至 18 世紀:統計學嘅英文名 statistics 係源自
德文入面 statistik 呢個字最早係喺 1749 年有人用嘅,代表對國家嘅數據做分析嘅一門學問,亦即係「研究國家嘅科學」;清朝末期(19 世紀尾到廿世紀初),唐人學者將西學引入大中華地區,作咗統計呢個詞語嚟代表呢門研究數據嘅學術,俾人一路沿用到而家[65][66]。
睇埋
編輯註釋
編輯文獻
編輯- Cohen, J. (1990). Things I have learned (so far). American Psychologist, 45, 1304-1312.
- Barbara Illowsky; Susan Dean (2014). Introductory Statistics. OpenStax CNX. ISBN 9781938168208.
- Stephen Jones, (2010). Statistics in Psychology: Explanations without Equations. Palgrave Macmillan. ISBN 9781137282392.
- Stockburger, David W. "Introductory Statistics: Concepts, Models, and Applications". Missouri State University (3rd Web ed.). Archived from the original on 28 May 2020.
- OpenIntro Statistics, 3rd edition by Diez, Barr, and Cetinkaya-Rundel
- Gigerenzer, G (2004). "Mindless statistics". Journal of Socio-Economics. 33: 587–606. doi:10.1016/j.socec.2004.09.033.
- Ioannidis, J.P.A. (2005). "Why most published research findings are false". PLoS Medicine. 2: 696–701. doi:10.1371/journal.pmed.0040168. PMC 1855693. PMID 17456002.
參考
編輯- ↑ philosophy of science
- ↑ approximately accurate models
- ↑ inductive reasoning
- ↑ probability
- ↑ descriptive
- ↑ inferential
- ↑ data collection
- ↑ variable
- ↑ continuous variable
- ↑ discrete variable
- ↑ sampling
- ↑ statistical population
- ↑ Homo sapien
- ↑ sample
- ↑ generalize
- ↑ IQ test
- ↑ level of measurement
- ↑ nominal
- ↑ ordinal
- ↑ interval
- ↑ ratio
- ↑ reliability
- ↑ validity
- ↑ dataset
- ↑ mean
- ↑ variance
- ↑ standard deviation
- ↑ probability distribution
- ↑ mathematical function
- ↑ normal distribution
- ↑ bell curve
- ↑ independent and identically distributed,IID
- ↑ independent
- ↑ correlational
- ↑ experimental
- ↑ statistical correlation
- ↑ Pearson correlation coefficient
- ↑ causality
- ↑ correlation does not imply causation
- ↑ manipulate
- ↑ controlled environment
- ↑ experimental group
- ↑ control group
- ↑ Hawthorne effect
- ↑ hypothesis testing
- ↑ parameter
- ↑ estimator
- ↑ confidence interval,CI
- ↑ null hypothesis
- ↑ alternative hypothesis
- ↑ Type I Error
- ↑ false positive
- ↑ Type II Error
- ↑ false negative
- ↑ statistical significance
- ↑ reject the null hypothesis
- ↑ comparison of means
- ↑ Student's t-test
- ↑ independent samples t-test
- ↑ paired samples t-test / repeated-measure t-test
- ↑ analysis of variance,ANOVA
- ↑ one-way ANOVA
- ↑ Darrell Huff
- ↑ 英:Manuscript on Deciphering Cryptographic Messages
- ↑ Giovanni Villani
- ↑ John Graunt
- ↑ 1.0 1.1 1.2 Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p.xii, ISBN 978-0-03-077945-9
- ↑ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5 . pp. 1-3
- ↑ Etikan, I., & Bala, K. (2017). Sampling and sampling methods. Biometrics & Biostatistics International Journal, 5(6), 00149.
- ↑ Stevens, S. S. (7 June 1946). "On the Theory of Scales of Measurement". Science. 103 (2684): 677–680.
- ↑ Michell, J (1986). "Measurement scales and statistics: a clash of paradigms". Psychological Bulletin. 100 (3): 398–407.
- ↑ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, Oxford University Press. ISBN 0-19-920613-9
- ↑ Romijn, Jan-Willem (2014). "Philosophy of statistics". Stanford Encyclopedia of Philosophy.
- ↑ Halvorson, H. O., & Ziegler, N. R. (1933). Application of statistics to problems in bacteriology: I. A means of determining bacterial population by the dilution method. Journal of Bacteriology, 25(2), 101.
- ↑ Lumb, P. (1974). Application of statistics in soil mechanics. Soil Mechanics New Horizons. IK Lee, ed.
- ↑ Stanovich, Keith E. (2007). How to Think Straight About Psychology. Boston: Pearson Education. p. 123
- ↑ Crawford S., Stucki L. (1990), "Peer review and the changing research record", J Am Soc Info Science, vol. 41, pp. 223–28
- ↑ Godfrey-Smith 2003, Chapter 14: "Bayesianism and Modern Theories of Evidence".
- ↑ Sklar, L. (1992). Philosophy of physics. Dimensions of Philosophy S.
- ↑ Brigandt, Ingo; Love, Alan (2017), "Reductionism in Biology", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2017 ed.), Metaphysics Research Lab, Stanford University.
- ↑ Deductive and Inductive Arguments.
- ↑ Sextus Empiricus, Outlines of Pyrrhonism. Trans. R.G. Bury, Harvard University Press, Cambridge, Massachusetts, 1933, p. 283.
- ↑ There's No Such Thing As Proof In The Scientific World - There's Only Evidence. Forbes.
- ↑ Chance, Beth L.; Rossman, Allan J. (2005). "Preface". Investigating Statistical Concepts, Applications, and Methods (PDF). Duxbury Press. ISBN 978-0-495-05064-3.
- ↑ Moore, David (1992). "Teaching Statistics as a Respectable Subject". In F. Gordon and S. Gordon. Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14-25.
- ↑ William Feller, An Introduction to Probability Theory and Its Applications, (Vol 1), 3rd Ed, (1968), Wiley.
- ↑ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston
- ↑ Moore, David (1992). "Teaching Statistics as a Respectable Subject". Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14–25. ISBN 978-0-88385-078-7.
{{cite book}}: Unknown parameter|editors=ignored (|editor=suggested) (help) - ↑ Moses, Lincoln E. (1986). Think and Explain with Statistics, Addison-Wesley.
- ↑ Descriptive & Inferential Statistics: Definition, Differences & Examples.
- ↑ Pearcey, S. M., & De Castro, J. M. (2002). Food intake and meal patterns of weight-stable and weight-gaining persons. The American journal of clinical nutrition, 76(1), 107-112.
- ↑ Lescroël, A. L.; Ballard, G.; Grémillet, D.; Authier, M.; Ainley, D. G. (2014). Descamps, Sébastien (ed.). "Antarctic Climate Change: Extreme Events Disrupt Plastic Phenotypic Response in Adélie Penguins". PLoS ONE. 9 (1): e85291.
- ↑ Michell, J. (1993). The origins of the representational theory of measurement: Helmholtz, Hölder, and Russell. Studies in History and Philosophy of Science, 24, 185-206.
- ↑ K.D. Joshi, Foundations of Discrete Mathematics, 1989, New Age International Limited, [1], page 7.
- ↑ Stuart, A. (1962). Basic Ideas of Scientific Sampling. New York: Hafner Publishing Company.
- ↑ "Psychology Secrets: Most Psychology Studies Are College Student Biased". 原著喺2017年7月6號歸檔. 喺2017年12月3號搵到.
- ↑ "Levels of measurement". 原著喺2017年11月27號歸檔. 喺2017年11月26號搵到.互聯網檔案館嘅歸檔,歸檔日期2017年11月27號,.
- ↑ Kirch, W., ed. (2008). "Level of Measurement". Encyclopedia of Public Health. Springer. pp. 851–852.
- ↑ Furr, R. M. (2017). Psychometrics: an introduction. Sage Publications.
- ↑ Nunnally, J.C. (1978). Psychometric theory (2nd ed.). New York: McGraw-Hill.
- ↑ Data, C. E., & Using Descriptive Statistics Bartz, A. E. (1988). Basic statistical concepts. New York: Macmillan. Devore, J., and Peck.
- ↑ B. S. Everitt: The Cambridge Dictionary of Statistics, Cambridge University Press, Cambridge (3rd edition, 2006).
- ↑ Bryc, Wlodzimierz (1995). The Normal Distribution: Characterizations with Applications. Springer-Verlag.
- ↑ Dinov, Ivo; Christou, Nicolas; Sanchez, Juana (2008). "Central Limit Theorem: New SOCR Applet and Demonstration Activity". Journal of Statistics Education. ASA. 16 (2).
- ↑ Freedman, D.A. (2005). Statistical Models: Theory and Practice, Cambridge University Press.
- ↑ Rodgers, J. L.; Nicewander, W. A. (1988). "Thirteen ways to look at the correlation coefficient". The American Statistician. 42 (1): 59-66.
- ↑ Aldrich, John (1995). "Correlations Genuine and Spurious in Pearson and Yule" (PDF). Statistical Science. 10 (4): 364–376.
- ↑ 42.0 42.1 Alvin E. Roth, 2002. "The Economist as Engineer: Game Theory, Experimentation, and Computation as Tools for Design Economics," Econometrica, 70(4), pp. 1341–1378.
- ↑ See, e.g., Grechenig, K., Nicklisch, A., & Thöni, C. (2010). Punishment despite reasonable doubt—a public goods experiment with sanctions under uncertainty. Journal of Empirical Legal Studies, 7(4), 847-867.
- ↑ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P (2007). "The Hawthorne Effect: a randomised, controlled trial". BMC Med Res Methodol. 7 (1): 30.
- ↑ 45.0 45.1 Myers, Jerome L.; Well, Arnold D.; Lorch Jr., Robert F. (2010). "Developing fundamentals of hypothesis testing using the binomial distribution". Research design and statistical analysis (3rd ed.). New York, NY: Routledge. pp. 65–90.
- ↑ Jaynes, E. T. (2007), Probability Theory: The logic of science (5 ed.), Cambridge University Press,
- ↑ Zar, J. H. (1984). Biostatistical Analysis. Prentice-Hall International, New Jersey, pp 43–45.
- ↑ Adèr, H. J.; Mellenbergh, G. J. & Hand, D. J. (2007). Advising on research methods: A consultant's companion. Huizen, The Netherlands: Johannes van Kessel Publishing.
- ↑ Everitt, B. (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 0521593468.
- ↑ Rubin, D. B.; Little, R. J. A. (2002). Statistical analysis with missing data. New York: Wiley.
- ↑ The Difference Between Type I and Type II Errors.
- ↑ Lydia Denworth, A Significant Problem: Standard scientific methods are under fire. Will anything change?, Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. "The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields... Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining "significant" results." (p. 63.),呢篇文講到:「(自從 1925 年)近一個世紀以嚟,用 p 值決定一個實驗結果係咪顯著,搞到我哋有種肯定嘅錯覺(有種錯覺以為可以肯定啲實驗結果係啱嘅)同引起咗好多科學領域嘅再現危機(指實驗結果做唔到再現)... 有啲研究者主張改變用緊嘅統計方法,而其他就會放棄唔再用門檻值嚟界定『顯著』嘅結果。」
- ↑ Piazza E. (2007). Probabilità e Statistica. Esculapio.
- ↑ O'Mahony, M. (1986). Sensory Evaluation of Food: Statistical Methods and Procedures. CRC Press. p. 487. ISBN 0-82477337-3.
- ↑ 55.0 55.1 55.2 Derrick, B; Toher, D; White, P (2017). "How to compare the means of two samples that include paired observations and independent observations: A companion to Derrick, Russ, Toher and White (2017)". The Quantitative Methods for Psychology. 13 (2): 120–126.
- ↑ McCulloch, J. Huston (1985). "On Heteroscedasticity". Econometrica. 53 (2): 483.
- ↑ Howell, David (2002). Statistical Methods for Psychology. Duxbury. pp. 324–325.
- ↑ 英文段原文:"There are three kinds of lies: lies, damned lies, and statistics."
- ↑ Huff, D. (1954). How to Lie With Statistics, WW Norton & Company, Inc. New York, NY. ISBN 978-0-393-31072-6
- ↑ Drennan, R. D. Statistics in archaeology. (Edit) Pearsall, Deborah M. Encyclopedia of Archaeology. Elsevier Inc. 2008: 2093–2100.
- ↑ Cohen, J. B. Misuse of Statistics. Journal of the American Statistical Association (JSTOR). 1938年12月, 33 (204): 657–674.
- ↑ Al-Kadi, I. A. (1992) "The origins of cryptology: The Arab contributions", Cryptologia, 16(2) 97–126. doi:10.1080/0161-119291866801
- ↑ Singh, S. (2000). The code book : the science of secrecy from ancient Egypt to quantum cryptography (1st Anchor Books ed.). New York: Anchor Books.
- ↑ Willcox, W. (1938) "The Founder of Statistics". Review of the International Statistical Institute, 5(4):321–328.
- ↑ 《文明小史.第四八回》:「所賺雖只毫釐,積少成多,一年統計,卻也不在少數。」
- ↑ 〈詞條名稱:統計〉. 《教育部重編國語辭典修訂本》. 臺灣教育部. 原著喺2020年3月28號歸檔. 喺2018年5月15號搵到.