前饋神經網絡

前饋神經網絡cin4 gwai3 san4 ging1 mong5 lok6（英文：feedforward neural network）係最簡單最早期嗰種人工神經網絡。一個前饋神經網絡會有一浸輸入層（input）同一浸輸出層（output），亦可能有一浸隱藏層（hidden）。每一粒神經細胞都有條噉嘅式：

一個前饋人工神經網絡嘅抽象圖；每個圓圈代表一粒神經細胞，每粒神經細胞嘅啟動程度淨係受佢打前嗰排神經細胞嘅啟動程度影響。

$t=W_{1}A_{1}+W_{2}A_{2}...$；（啟動函數）

喺呢條式當中，$t$ 代表嗰粒神經細胞嘅啟動程度，$A_{n}$ 代表前一排嘅神經細胞當中第 $n$ 粒嘅啟動程度，而 $W_{n}$ 就係其他神經細胞當中第 $n$ 粒嘅權重（指嗰粒神經細胞有幾影響到 $t$）。$A_{n}$ 當中唔包括任何前排以外嘅細胞，令成個網絡嘅訊號只會以一個方向傳遞－呢一點令前饋神經網絡好唔似生物神經網絡，亦都係前饋網絡同遞迴神經網絡（RNN）嘅主要差異。

雖然係噉，事實說明咗前饋神經網絡能夠輕易處理非連串性（non-sequential；一串文字就有連串性－前面嘅資訊會影響後面嘅資訊嘅意思）而且唔視乎時間（一個視乎時間嘅數據帶嘅資訊會受時間影響，${\text{info}}=f({\text{time}})$）嘅數據，例如有遊戲 AI 方面嘅研究者試過成功噉訓練一部多層感知機（睇下面）玩食鬼。所以就算到咗廿一世紀，前饋神經網絡都仲有人用。

單層感知機

一個極之簡單嘅前饋神經網絡，得嗰兩個 input 同埋一個 output。

内文：感知機

感知機（perceptron）係最簡單嗰種前饋神經網絡做法。感知機喺機械學習上泛指用監督式學習嚟做二元分類（binary classification）嘅演算法，即係攞若干個個案，將每個個案分做兩個類別嘅其中一類，例如攞若干幅相，將啲相分類做貓（0）同狗（1）噉。感知機呢樣嘢可以用簡單嘅前饋神經網絡實現，家陣想像以下呢個噉嘅前饋網絡：

• 有兩個 input，同埋
• 一個 output，
• 冇隱藏層。

即係話，

${\text{output}}={\begin{cases}1&{\text{if }}{\text{condition}}_{1},\\0&{\text{if }}{\text{condition}}_{0}.\end{cases}}$

當中「${\text{condition}}_{1}$」係被歸類做「1」要達到嘅條件（例如 input A = 1 而且 input B = 0），而「${\text{condition}}_{0}$」係被歸類做「0」要達到嘅條件（例如 input A = 0 而且 input B = 1）。

想像兩個 input 係兩個變數，而 output 就係個個案屬嘅類別，例如按「有冇毛」同「有冇鱗片」呢兩個變數（input）將一隻動物分做哺乳類（0）同爬蟲類（1）兩種，假設權重正確而且哺乳類同爬蟲類之間條分界真係咁簡單，呢部感知機將會能夠做到「將動物分類嘅工作」。

而廣義上，一部感知機嘅輸出可以想像成以下呢條式：

${\text{output}}=g({\overrightarrow {w}}\cdot {\overrightarrow {x}}+b)$；$[1]$

當中 ${\overrightarrow {x}}$ 係代表柞輸入嘅向量；${\overrightarrow {w}}$ 係代表柞權重嘅向量；而 $b$ 代表偏向（bias），即係嗰粒神經細胞本身喺啟動上嘅傾向，例如如果有某一粒人工神經細胞嘅 $b$ 係正數而且數值大，佢就會傾向無論輸入係幾多都有強烈嘅啟動。用嘅係監督式學習，個學習演算法要做嘅嘢就係按讀取到嘅數值調整柞 $w$，等個網絡將來會更加有能力俾到準確嘅輸出。

例子碼

例如以下呢段用 Python 程式語言寫嘅源碼定義咗一個簡單嘅感知機神經網絡：

def Perceptron(input1, input2, output) : # 定義一個網絡，個網絡有兩個輸入同埋一個輸出。
   outputP = input1*weights[0] + input2*weights[1] + biais*weights[2] # 個網絡嘅輸出條式
   if outputP > 0 : #activation function (here Heaviside) # 如果個輸出值大過 0，噉將輸出值 set 做 1。
      outputP = 1
   else :
      outputP = 0 # 呢個網絡係一個開關網絡，即係話佢輸出值淨係得兩個可能性，「0」同「1」。

誤差函數

睇埋：損失函數

要教部感知機學習，通常第一步係要界定一個誤差函數（error function）。學習定義上係指按照經驗改變自己嘅行為，所以一個認知系統要學習，其中一個最直接嘅做法係睇吓自己做嘅預測同實際經驗到嘅有幾大差異，誤差函數係指一個表達誤差（error）由邊啲變數同常數話事嘅函數（function），例如以下呢個就係一個常用嘅誤差函數：

$E(X)={\frac {1}{N}}\sum _{i=1}^{N}({\text{output}}_{i}-y_{i})^{2}$；$[2]$（均方誤差；mean squared error）

$E(X)={\frac {1}{N}}\sum _{i=1}^{N}(g({\overrightarrow {w}}\cdot {\overrightarrow {x}}+b)-y_{i})^{2}$；$[3]$（代咗 $[1]$ 入去 $[2]$ 嗰度）

呢條式當中嘅 $E(X)$ 反映咗個總誤差：$({\text{output}}_{i}-y_{i})^{2}$ 表示第 $i$ 個預測（${\text{output}}_{i}$）同第 $i$ 個實際經驗到嘅數值（$y_{i}$）之間嘅差異，呢個數字嘅次方一定會係正數，所以將所有次數嘅誤差加埋就會反映部感知機做咗 $N$ 次預測之後嘅總誤差。如果每次嘅預測都同實際經驗到嘅數值一樣（${\text{output}}_{i}=y_{i}$），$E(X)=0$。喺呢個情況下，一個學習演算法要做嘅嘢就係改變柞 $w$ 嘅數值同埋 $b$，務求最後令到 $E(X)$ 嘅數值有咁細得咁細。

Delta 法則

内文：Delta 法則

Delta 法則（delta rule）係一種用嚟計一部感知機啲權重要點樣調整嘅方法，係反向傳播算法（睇下面）嘅一個特殊例子。喺得到誤差函數之後，就可以計柞 $w$ 要點調整，即係以下呢條算式嚟計出每個權重值 $w_{ij}$ 要點樣按誤差變：

$w_{ij}(t+1)=w_{ij}(t)+\eta {\frac {\partial E(X)}{\partial w_{ij}}}$；$[4]$ 當中

• $w_{ij}(n)$ 係指喺時間點 $n$ 嘅權重值 $w_{ij}$；
• $\eta$ 係學習率（learning rate）；
• $E(X)$ 係個誤差，反映咗喺個個案入面個神經網絡俾嘅輸出同正確輸出差幾遠；
• ${\frac {\partial E(X)}{\partial w_{ij}}}$ 係 $E(X)$ 隨住 $w_{ij}$ 嘅偏導數（partial derivative）。

訓練演算法

訓練部感知機嘅演算法大致如下：

第一步：傳播

1. 由數據嗰度邏一個個案，按照個神經網絡嘅權重同埋個個案嘅輸入值計個神經網絡會俾啲乜嘢輸出值（用 $[1]$ 計出 ${\text{output}}_{i}$）；
2. 計吓個誤差係幾多（用 $[2]$ 計 $({\text{output}}_{i}-y_{i})^{2}$ 同 $E(X)$）；
3. 用條式計吓每個權重數值應該要變幾多（用 $[4]$ 計 $w_{ij}(t+1)$）。

第二步：更新權重值

1. 每一個權重值，佢都會由條式嗰度有一個梯度值（gradient）；
2. 每一個權重值嘅改變幅度等如個梯度值乘以 $\eta$－如果 $\eta$ 係 0，噉個神經網絡永遠都唔會變，而如果 $\eta$ 數值大，噉個神經網絡會變化得好快，所以 $\eta$ 掌管咗個神經網絡學習有幾快；
3. 將邇柞值「反向傳播」返去個神經網絡嗰度，將每個權重值變成佢嘅新數值（實際更新 $w_{ij}$ 值）；
4. 重複以上步驟，理想嘅係直至誤差值變成 0 為止，或者係變到一個接受得到嘅程度。可以睇埋過適。

順利嘅話，經過呢個步驟之後，部感知機就會有能力對未來遇到嘅個案作出有返咁上下準嘅預測。

局限

單層感知機（single-layer perceptron；冇隱藏層嘅感知機）嘅局限在於佢係線性嘅分類機。單層感知機嘅感知機只能夠學識作出線性嘅分類，即係例如按兩個變數 $x$ 同 $y$ 將一柞個案分類，一個分類機會畫一條線，而條線係 $x$ 同 $y$ 嘅函數（例：$y=2x+5$），如果呢條線能夠正確噉分開兩類個案，條線就係一部成功嘅線性分類機（linear classifier）；根據研究，單層感知機淨係處理得到線性（linear）嘅關係，如果個實際關係唔係線性，單層感知機就會搞唔掂。想像以下呢兩幅圖：

每個圓圈代表一個個案，個個案喺 x（X 軸）同 y（Y 軸）呢兩個變數上都有個數值，黑點同白點係兩類唔同個案，一個有效嘅分類機要畫一條線，分開兩類個案。右圖嘅情況可以用線性分類機搞得掂－黑點同白點可以用一條直線（一個線性嘅函數）分開；但左圖嘅情況線性分類機就會搞唔掂－啲黑點同白點要用一條曲線（一個非線性嘅函數）先至會分得開，呢類情況就冇得用（頂櫳會識線性分類嘅）單層感知機解決。

多層感知機

内文：多層感知機

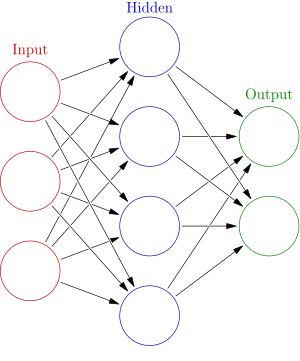
多層感知機（multi-layer perceptron，MLP）係一個包含多部感知機嘅人工神經網絡：多層感知機有隱藏層（hidden layer），即係唔會直接收外界輸入又唔會直接向外界俾輸出嘅神經細胞層；同單層感知機唔同嘅係，多層感知機能夠處理非線性嘅關係，喺好多人工神經網絡應用上都有價值。一部三層（有一浸隱藏層）嘅感知機可以想像成以下噉嘅樣：

圖入面每個圓圈代表一粒神經細胞，而 A 有箭咀去 B 表示 B 嘅啟動程度受 A 嘅影響。

定義上，多層感知機具有以下嘅特徵：

• 每粒第 $i$ 層嘅神經細胞都同第 $i-1$ 層嘅神經細胞有連繫，即係話每粒第 $i-1$ 層嘅神經細胞都有能力影響第 $i$ 層嘅神經細胞嘅啟動程度，即係每層之間都完全連繫，不過權重值可以係 0；
• 第 $i$ 層嘅神經細胞唔會受第 $j$ 層嘅神經細胞影響，當中 $j$ 係任何一個大過 $i$ 嘅整數；
• 同一層嘅神經細胞之間冇連繫。

反向傳播算法

内文：反向傳播算法

反向傳播算法（backpropagation）係 delta 法則（睇上面）嘅廣義化：喺得到誤差函數之後，就可以計柞 $w$ 要點調整，例如隨機梯度下降法（stochastic gradient descent）噉，就會運用以下呢條算式嚟計出每個權重值要點變：

$w_{ij}(t+1)=w_{ij}(t)+\eta {\frac {\partial E(X)}{\partial w_{ij}}}+\xi (t)$；$[5]$ 當中

• $w_{ij}(n)$ 係指喺時間點 $n$ 嘅權重值 $w_{ij}$；
• $\eta$ 係學習率；
• $E(X)$ 係個誤差，反映咗喺個個案入面個神經網絡俾嘅輸出同正確輸出差幾遠；
• ${\frac {\partial E(X)}{\partial w_{ij}}}$ 係 $E(X)$ 隨住 $w_{ij}$ 嘅偏導數（partial derivative）；
• $\xi (t)$ 係一個隨機嘅數值。

如果一個以電腦程式寫嘅神經網絡跟呢條式（或者係類似嘅式）嚟行嘅話，佢喺計完每一個個案之後，都會計出佢裏面嘅權重值要點樣改變，並且將呢個「每個權重應該要點變」嘅資訊傳返去個網絡嗰度（所以就叫「反向傳播」）。而每次有個權重值改變嗰陣，佢嘅改變幅度會同「誤差值」有一定嘅關係，而且佢對計個輸出嘅參與愈大，佢嘅改變幅度會愈大－個神經網絡會一路計個案一路變，變到誤差值愈嚟愈接近零為止。而除咗確率勾配降下法之外，反向傳播仲有好多其他方法做，詳情可以睇最佳化（optimization）相關嘅課題。

多層感知機嘅訓練演算法同單層感知機嘅基本上一樣。

例子碼

以下係一個用 C# 整嘅多層感知機網絡源碼（「initialize」係指初始化）：

private int[] layers; // layers    
private float[][] neurons; // neurons    
private float[][] biases; // biasses    
private float[][][] weights; // weights    
private int[] activations; // layers
public float fitness = 0; // fitness

public NeuralNetwork(int[] layers)
{        
  this.layers = new int[layers.Length];        
  for (int i = 0; i < layers.Length; i++)        
  {            
    this.layers[i] = layers[i];        
  }        
  InitNeurons();        
  InitBiases();        
  InitWeights();    
}

private void InitNeurons() // Initialize neurons
{        
  List<float[]> neuronsList = new List<float[]>();        
  for (int i = 0; i < layers.Length; i++)        
  {            
    neuronsList.Add(new float[layers[i]]);        
  }        
  neurons = neuronsList.ToArray();    
}

private void InitBiases() // Initialize biases
{        
  List<float[]> biasList = new List<float[]>();        
  for (int i = 0; i < layers.Length; i++)        
  {            
    float[] bias = new float[layers[i]];            
    for (int j = 0; j < layers[i]; j++)            
    {                
      bias[j] = UnityEngine.Random.Range(-0.5f, 0.5f);            
    }            
    biasList.Add(bias);        
  }        
  biases = biasList.ToArray();    
}

private void InitWeights() // Initialize weights
{        
  List<float[][]> weightsList = new List<float[][]>();        
  for (int i = 1; i < layers.Length; i++)        
  {            
    List<float[]> layerWeightsList = new List<float[]>();   
    int neuronsInPreviousLayer = layers[i - 1];            
    for (int j = 0; j < neurons[i].Length; j++)            
    {                 
      float[] neuronWeights = new float[neuronsInPreviousLayer];
      for (int k = 0; k < neuronsInPreviousLayer; k++)  
      {                                      
        neuronWeights[k] = UnityEngine.Random.Range(-0.5f, 0.5f); 
      }               
      layerWeightsList.Add(neuronWeights);            
    }            
    weightsList.Add(layerWeightsList.ToArray());        
  }        
  weights = weightsList.ToArray();    
}

然後以下呢段碼就可以幫由做「feedforward」，由 inputs 計 outputs 出嚟：

public float[] FeedForward(float[] inputs)
{        
  for (int i = 0; i < inputs.Length; i++)        
  {            
    neurons[0][i] = inputs[i];        
  }        
  for (int i = 1; i < layers.Length; i++)        
  {            
    int layer = i - 1;            
    for (int j = 0; j < neurons[i].Length; j++)            
    {                
      float value = 0f;               
      for (int k = 0; k < neurons[i - 1].Length; k++)  
      {                    
        value += weights[i - 1][j][k] * neurons[i - 1][k];      
      }                
    neurons[i][j] = activate(value + biases[i][j]);            
    }        
  }        
  return neurons[neurons.Length - 1];    
}

如果用嚟做學習嘅係遺傳演算法（genetic algorithm）：

// 比較兩個神經網絡嘅表現
public int CompareTo(NeuralNetwork other)    
{        
  if (other == null) 
    return 1;    
  if (fitness > other.fitness)            
    return 1;        
  else if (fitness < other.fitness)            
    return -1;        
  else            
    return 0;    
}

// 整一個新嘅網絡出嚟；一般係要個新網絡似表現好啲嗰個網絡。
public void Load(string path)
{        
  TextReader tr = new StreamReader(path);        
  int NumberOfLines = (int)new FileInfo(path).Length;        
  string[] ListLines = new string[NumberOfLines];        
  int index = 1;        
  for (int i = 1; i < NumberOfLines; i++)        
  {            
    ListLines[i] = tr.ReadLine();        
  }        
  tr.Close();        
  if (new FileInfo(path).Length > 0)        
  {            
    for (int i = 0; i < biases.Length; i++)            
    {               
      for (int j = 0; j < biases[i].Length; j++)                
      {                    
        biases[i][j] = float.Parse(ListLines[index]); 
        index++;                                   
      }            
    }             
    for (int i = 0; i < weights.Length; i++)            
    {                
      for (int j = 0; j < weights[i].Length; j++)                
      {                    
        for (int k = 0; k < weights[i][j].Length; k++)
        {                        
          weights[i][j][k] = float.Parse(ListLines[index]);    
          index++;                                        
        }                
      }            
    }        
  }    
}

// 突變，令網絡「繁殖」嗰陣有些少隨機性嘅變化。
public void Mutate(int chance, float val)    
{        
  for (int i = 0; i < biases.Length; i++)        
  {            
    for (int j = 0; j < biases[i].Length; j++)            
    {                
      biases[i][j] = (UnityEngine.Random.Range(0f, chance) <= 5) ? biases[i][j] += UnityEngine.Random.Range(-val, val) : biases[i][j]; 
    }        
  }  
       
  for (int i = 0; i < weights.Length; i++)        
  {            
    for (int j = 0; j < weights[i].Length; j++)            
    {                
      for (int k = 0; k < weights[i][j].Length; k++)                
      {                    
        weights[i][j][k] = (UnityEngine.Random.Range(0f, chance) <= 5) ?  weights[i][j][k] += UnityEngine.Random.Range(-val, val) : weights[i]  [j][k];
                
      }            
    }        
  }    
}

如果一切順利，行完若干次「複製表現好啲嗰個網絡」之後，最後會得出一個極擅長做預測嘅網絡。

研究

喺人工神經網絡研究上，研究者好多時都會想探討一啲有關前饋神經網絡應用嘅問題。呢啲研究通常嘅做法係，製作幾個喺某啲參數－包括輸入層嘅細胞數量、輸出層嘅細胞數量、隱藏層嘅數量以及隱藏層嘅細胞數量呀噉－上有差異嘅前饋神經網絡，然後 foreach 網絡，訓練個網絡學習，最後睇吓個網絡嘅表現（例如學習完後做預測嘅準確度）。例如係以下呢份研究噉：

• 研究者想製作前饋網絡，用嚟幫手診斷心臟方面嘅病；
• 佢哋製作咗 6 個唔同嘅前饋神經網絡，呢 6 個網絡分做兩組，
  • 其中 4 個網絡係第一組，4 個都係普通就噉一個前饋網絡，呢 4 個前饋網絡喺輸入層嘅細胞數量、輸出層嘅細胞數量、隱藏層嘅數量等參數上有所不同；
  • 另外 2 個網絡係第二組，每個都分別係由兩個多層感知機組成嘅兩階段複合前饋網絡，呢 2 個複合前饋網絡都係喺嗰啲參數上唔同；
• 佢哋手上有個數據庫，個數據庫有柞數據，包括量度心臟活動嘅架生得到嘅數據同埋「個病人係咪有病」嘅數據；
• 以量度心臟活動嘅架生得到嘅數據做輸入，「個病人係咪有病」做輸出，行一個監督式學習；
• Foreach 網絡，佢哋睇吓個網絡做完學習之後做預測嘅準確性係點。佢哋發現複合前饋網絡嘅表現好過普通就噉一個前饋網絡嘅－所以佢哋就發現咗一啲有用嘅嘢，可以將佢哋嘅研究成果喺有關機械學習嘅學術期刊上公佈。

睇埋

• 人工神經網絡
• 遞迴神經網絡
• 反向傳播算法
• 機械學習
• 自編碼器；喺最簡單嗰種情況下，一個自編碼器係以輸入做預想輸出、隱藏層細胞數量少嘅前饋網絡。

文獻

• Abu Dalffa, M., Abu-Nasser, B. S., & Abu-Naser, S. S. (2019). Tic-Tac-Toe Learning Using Artificial Neural Networks (PDF).
• Bhaskar, K., & Singh, S. N. (2012). AWNN-assisted wind power forecasting using feed-forward neural network (PDF). IEEE transactions on sustainable energy, 3(2), 306-315.
• Valian, E., Mohanna, S., & Tavakoli, S. (2011). Improved cuckoo search algorithm for feedforward neural network training. International Journal of Artificial Intelligence & Applications, 2(3), 36-43.

拎

• Feedforward neural networks tutorial.
• Feedforward Neural Network: Example.
• Feedforward Neural Networks: An Introduction.