甘別分佈

甘別分佈（英文：Gumbel distribution，又叫Generalized Extreme Value distribution Type-I，「1型廣義極值分佈」）係喺概率論同統計學當中幫個最大值（或者最細值）建模嘅分佈、個最值係喺各式分佈啲一堆樣本之中攞出嘅。

Gumbel

概率密度函數
累積分佈函數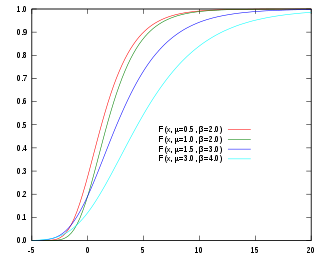
變數	$\mu ,$ location (real) $\beta >0,$ scale (real)
撐集	$x\in \mathbb {R}$
PDF	${\frac {1}{\beta }}e^{(z-e^{z})}$ where $z={\frac {x-\mu }{\beta }}$
CDF	$e^{-e^{-(x-\mu )/\beta }}$
平均數	$\mu +\beta \gamma$ where $\gamma$ is the Euler–Mascheroni constant
中位數	$\mu -\beta \ln(\ln 2)$
眾數	$\mu$
方差	${\frac {\pi ^{2}}{6}}\beta ^{2}$
偏度	${\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14$
峰度	${\frac {12}{5}}$
熵	$\ln(\beta )+\gamma +1$
MGF	$\Gamma (1-\beta t)e^{\mu t}$
CF	$\Gamma (1-i\beta t)e^{i\mu t}$

呢個分佈係可以表示得出特定年份江水最高水位嘅分佈，若果有返幅表有過去十年啲最大值嘅話。個分佈有助於預測啲極端地震、洪水或者其他自然災害發生嘅可能性。甘別分佈個潛在適用性、攞嚟表示最大值分佈嘅係同極值理論有關，個理論表明若果基礎樣本數據嘅分佈係正態或者指數類型，甘別分佈即可能會好有用。以下啲例都係使甘別分佈嚟建模畀個最大值嘅分佈。要建模畀個最細值，係使啲原始值嘅負數。

甘別分佈係廣義極值分佈（亦都喊做 Fisher-Tippett 分佈）嘅一個特例。佢亦都着喊做對數Weibull分佈同雙指數分佈（個術語有時亦都攞嚟指拉普拉斯分佈）。甘別分佈同甘佩茲分佈有關：個密度先圍原點反射、再限制喺正半線上嗰陣，就得到甘佩茲函數。

喺離散選擇理論裏便幾常見嘅係，啲潛在變數嘅誤差喺multinomial logit模型嘅潛在變數公式入便嘅係遵循返甘別分佈嘅。噉樣可以令到兩個甘別分佈個隨機變數差異有返邏輯分佈（logistic distribution）。

甘別分佈得名自Emil Julius Gumbel（1891 – 1966），基於佢篇原始論文描述到呢種分佈嘅。

定義

甘別分佈嘅累積分佈函數係：

$F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}$

標準甘別分佈

標準甘別分佈嘅情況係$\mu =0$同$\beta =1$具有累積分佈函數：

$F(x)=e^{-e^{(-x)}}\,$

同埋概率密度函數：

$f(x)=e^{-(x+e^{-x})}$

喺呢種情況下，眾數係 0，中位數係$-\ln(\ln(2))\approx 0.3665$ ，均值係$\gamma \approx 0.5772$ （ Euler-Mascheroni 常數），標準差係$\pi /{\sqrt {6}}\approx 1.2825.$

對於 n>1，累積量根據下式畀出：

$\kappa _{n}=(n-1)!\zeta (n)$

特性

眾數係 μ，中位數係$\mu -\beta \ln \left(\ln 2\right)$，平均值由下式畀出

$\operatorname {E} (X)=\mu +\gamma \beta$

其中$\gamma$係Euler-Mascheroni 常數。

標準差$\sigma$係$\beta \pi /{\sqrt {6}}$，所以掉轉頭有$\beta =\sigma {\sqrt {6}}/\pi \approx 0.78\sigma$。

喺眾數下，$x=\mu$ ， $F(x;\mu ,\beta )$個值變成$e^{-1}\approx 0.37$，即唔受$\beta$值影響。

相關分佈

• 若果$X$具有甘別分佈，係噉Y= − X嘅條件分佈具有甘佩茲分佈（假設Y係正，或者等效噉假設X係負）。Y嘅 cdf G同F （X嘅 cdf）有拏褦，對於y > 0有公式：$G(y)=P(Y\leq y)=P(X\geq -y|X\leq 0)=(F(0)-F(-y))/F(0)$；所以，密度同$g(y)=f(-y)/F(0)$相關：甘佩茲密度同反射嘅甘別密度成正比，僅衹限於正半線。
• 若果$X$有指數分佈、變數均值係 1 嘅，係噉− log( X ) 具有標準甘別分佈。
• 若果$X\sim \mathrm {Gumbel} (\alpha _{X},\beta )$同$Y\sim \mathrm {Gumbel} (\alpha _{Y},\beta )$係獨立嘅，係噉$X-Y$有邏輯分佈：$X-Y\sim \mathrm {Logistic} (\alpha _{X}-\alpha _{Y},\beta )\,$。
• 若果$X,Y\sim \mathrm {Gumbel} (\alpha ,\beta )$係獨立嘅，係噉$X+Y\nsim \mathrm {Logistic} (2\alpha ,\beta )$。注意$E(X+Y)=2\alpha +2\beta \gamma \neq 2\alpha =E\left(\mathrm {Logistic} (2\alpha ,\beta )\right)$。

廣義多元對數伽馬分佈相關理論提供咗甘別分佈嘅多元版本（multivariate version）。

應用

使用累積甘別分佈嘅置信帶擬合個分佈畀 10月最大嘅日降雨量。

甘別表明，個最大值（或者最孻順序統計量）喺啲服從指數分佈嘅隨機變數樣本之中攞出嘅、減去樣本size個自然對數嘅話隨樣本size愈大就愈發接近甘別分佈。

所以，喺水文學，甘別分佈着攞嚟分析諸如日降雨量同江水流量啲月份同年份最大值等變數，亦都着攞嚟描述啲乾旱。

甘別仲證明咗個對事件概率嘅估計量^r⁄_(n+1)（其中r係喺數據序列中觀察到嘅值嘅秩數，n係觀測值嘅總數）係一個無偏估計、估計返個累積概率圍住分佈嘅眾數嘅。所以，呢個估計量通常攞嚟做畫圖嘅中間位置。

喺數論，甘別分佈近似於個項數喺隨機整數拆分之中與及喺啲質數罅同埋啲質數宿（prime constellations）罅啲trend-adjusted sizes之中嘅。

喺機械學習，有時使用甘別分佈從啲分類分佈嚟生成返樣本。

計法

概率論文

一張包含甘別分佈嘅方格紙。

喺前軟件時代，甘別分佈係攞概率紙嚟描繪（見圖）。呢個論文基於累積分佈函數$F$嘅線性化：

$-\ln[-\ln(F)]=(x-\mu )/\beta$

喺論文入便，水平軸係攞雙對數刻度構建，而縱軸係線性嘅。畫個$F$喺紙嘅水平軸上， 畫$x$變數到縱軸上之後，個分佈就由斜率係 1 $/\beta$嘅直線表示到。等到類似CumFreq噉樣嘅分佈擬合軟件有得用嗰陣，繪製分佈嘅任務就變得容易咗啲，當中似下一節寫到噉生成甘別變數。

生成甘別變數

甘別分佈嘅分位數函數（逆累積分佈函數）$Q(p)$係由下式畀出：

$Q(p)=\mu -\beta \ln(-\ln(p))$

隨機變數$U$係從區間$(0,1)$嘅均勻分佈得出嗰陣，變數$Q(U)$即有帶參數$\mu$同$\beta$嘅甘別分佈。

睇埋

• 1型甘別分佈
• 2型甘別分佈
• 極值理論
• 廣義極值分佈
• Fisher–Tippett–Gnedenko定理
• Emil Julius Gumbel