線性判別分析

線性判別分析（粵音：sin3 sing3 pun3 bit6 fan1 sik1）係一種統計分析，能夠攞住若干個自變數，搵出一個有齊呢啲自變數嘅線性組合，再用呢個線性組合睇吓一拃個案有冇得清楚分做幾個類別。用日常用語講，線性判別分析做嘅係要計啲數值出嚟話畀分析者知，手上嗰幾個類別喺各種特性（自變數）上爭幾遠，仲有係邊個特性最能夠分辨呢幾個類別。

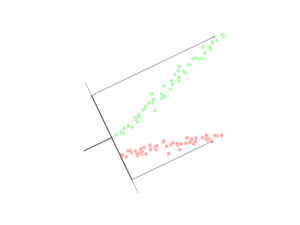
精確啲講，好似附圖 1 噉，附圖 1 係 2D 嘅，表示緊兩個自變數，幅圖上面每粒點點係一個個案，一粒點點嘅顏色表示佢屬邊個類別（類別都係有兩個）。由幅圖睇得出，粗嗰條線最能夠明顯噉分開兩個類別，組之間嘅差異（睇下面組間變異）沿住嗰條線最大化。條粗線就係線性判別分析想搵出嘅嘢。

線性判別分析嘅英文名叫 linear discriminant analysis，簡稱 LDA。

基本諗頭

LDA 係降維嘅一種常見做法。降維係指減低手上拃 data（dei1 taa4）入面隨機變數嘅數量，簡單例子可以想像而家要分析 1,000 隻蝴蝶，手上嘅 data 描述

	翼係咩形狀	色水係點	有乜花紋
蝴蝶 0001	噉噉噉	噉噉噉	噉噉噉
蝴蝶 0002	噉噉噉	噉噉噉	噉噉噉
蝴蝶 0003	噉噉噉	噉噉噉	噉噉噉

要做降維嘅話，就可能係按呢啲 data 將啲蝴蝶分做唔同嘅物種，噉就變成

	物種
蝴蝶 0001	物種 A
蝴蝶 0002	物種 B
蝴蝶 0003	物種 A

—令到啲 data 嘅維度下降咗，用日常用語講即係令啲 data 易睇咗。做科研或者教 AI 學習嗰陣，降維好多時都能夠令到啲 data 更易處理^[1]。而 LDA 就係降維會用到嘅一種技術。屬於一種監督式嘅做法^[2]。

初步模型

LDA 假設咗兩樣嘢：啲變數係成常態分佈嘅，而且唔同組嘅協方差矩陣都一樣樣。

以下計嘅數，簡化講可以想像成畫出一條線（搵自變數嘅線性組合），如果當咗呢條線係打橫嗰條軸嘅話，組之間嘅差異（組間差異）就會變到最大化，同時組內差異又要有咁細得咁細。

組間變異

首先，LDA 假定研究者已經知道晒每一個個案屬於邊個類別或者組。做以下嘅設定：想像家陣手上有拃 data ^[2]^:2.2，

X=\{x_{1},x_{2},...,x_{N}\}

，

當中 $N$ 係樣本嘥士，每個 $x$ 係樣本入面一個個案，而每個 $x$ 都有 $M$ 咁多個特性。樣本嘅個案可以分 $c$ 咁多類，每個個案都屬於呢 $c$ 類當中其中一類，每個個案「屬邊個類別」係已知嘅。

LDA 第一步係要計所謂嘅組間變異（ $S_{B}$ ），反映啲組之間差異有幾大。組 $i$ 嘅 $S_{B}$ （ $S_{Bi}$ ）就係

S_{B}=(m_{i}-m)^{2}=(W^{T}\mu _{i}-W^{T}\mu )^{2}

^{[詳解 1]}

總括嚟講，第一步得出「組之間爭幾遠」呢樣資訊。

組內變異

第二步就係要搵出組內變異（ $S_{W}$ ）。第 $j$ 組（ $\omega _{j}$ ）嘅組內變異（ $S_{Wj}$ ），可以想像成以下噉嘅式：

S_{Wj}=\sum _{x\in \omega _{j},j=1,...,c}(W^{T}x_{i}-m_{j})^{2}

^{[詳解 2]}

用日常用語講嘅話， $S_{Wj}$ 反映緊「第 $j$ 組內部嗰啲個體，彼此之間平均嚟講爭幾遠」呢一樣資訊。

出結果

知道咗 $S_{B}$ 同 $S_{W}$ 要點計之後，LDA 嘅目標就可以用以下嘅方式表述（費雪標準）：

\operatorname {argmax} {\frac {W^{T}S_{B}W}{W^{T}S_{W}W}}

S_{W}W=\lambda (S_{B}W)

當中 $\lambda$ 係特徵值。最基本上即係話，LDA 畫線（搵自變數嘅線性組合）嗰陣係想令到 $S_{B}$ 對 $S_{W}$ 呢個比例有咁大得咁大—組之間嘅差異要盡可能大，同時組內部嘅差異要盡可能細^[3]^[4]。

應用

做數據科學同統計等工作，成日都會用到 LDA 呢種技術。

例如營銷學嘅研究就有用 LDA 嚟分析消費者對產品或者服務嘅偏好：想像而家手上有 $c$ 咁多隻產品或者服務；研究者手上啲 data 描述嘅係客對嗰啲產品服務嘅觀感，即係啲 data 望落係噉嘅^[5]—

	用咗邊件產品	對產品畀幾多分	滿意度係幾多分
0001 號客仔	產品 A	4	3
0002 號客仔	產品 A	5	3.5
0003 號客仔	產品Ｂ	1	2

研究者跟住就可以行一場 LDA，睇吓唔同產品之間喺「客對件產品畀咗幾多分」同「客嘅滿意度係幾多分」等嘅特性上有幾大嘅差異（跟費雪標準）。

順帶一提，LDA 亦可以配合聚類分析嚟用：聚類分析做嘅都係將啲個案分類，不過唔使事先知道啲個案屬咩類別。研究者可以行咗聚類分析先，再行 LDA，睇吓兩者嘅結果係咪吻合，吻合嘅話就增強佢哋對聚類分析得出嘅結果嘅信心。除此之外，進階啲嘅 LDA 做法仲可以話畀分析者知，啲用嚟將啲個案分類嘅變數，邊啲比較重要邊啲冇咁重要，所以研究者可以行完聚類分析之後再行 LDA，睇吓將啲聚類分類嘅變數「邊啲比較有影響力」^[6]^[7]。

睇埋

詳解

↑ Tharwat, A., Gaber, T., Ibrahim, A., & Hassanien, A. E. (2017) 嗰篇文 2.2 嗰 part 有詳解呢條式，原版英文係："m_i represents the projection of the mean of the i-th class and it is calculated as follows, m_i = W^T µ_i, where m is the projection (投射) of the total mean of all classes (所有類別嘅整體平均) and it is calculated as follows, m = WT µ, W represents the transformation matrix (變換矩陣) of LDA, µ_i (1 × M) represents the mean of the i-th class."
↑ 有關呢啲數學符號嘅意思，可以睇睇加總同集合。

詞表

以下係篇文啲重要概念嘅粵英對照，啲拼音用嘅係粵拼：

降維 / gong3 wai4 / dimension reduction
類別 / leoi6 bit6 / class
組間變異 / zou2 gaan1 bin3 ji6 / between-class variance
組內變異 / zou2 noi6 bin3 ji6 / within-class variance
費雪標準 / fai3 syut3 biu1 zeon2 / Fisher's criterion
特徵值 / dak6 zing1 zik6 / eigenvalue
聚類分析 / zeoi6 leoi6 fan1 sik1 / cluster analysis

攷

↑ R. O. Duda, P. E. Hart, and D. G. Stork. Pattern classification. John Wiley & Sons, Second Edition, 2012.
↑ ^2.0 ^2.1 Tharwat, A., Gaber, T., Ibrahim, A., & Hassanien, A. E. (2017). Linear discriminant analysis: A detailed tutorial (PDF). AI communications, 30(2), 169-190，第一句就提到 dimensionality reduction 嘅概念。
↑ J. Ye, R. Janardan, and Q. Li. Two-dimensional linear discriminant analysis. In Proceedings of 17th Advances in Neural Information Processing Systems (NIPS), pages 1569-1576, 2004.
↑ J. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos. Face recognition using lda-based algorithms. IEEE Transactions on Neural Networks, 14(1):195-200, 2003.
↑ Bilgili, B., & Ozkul, E. (2015). Brand awareness, brand personality, brand loyalty and consumer satisfaction relations in brand positioning strategies (A Torku brand sample). Journal of Global Strategic Management| Volume, 9(2), 10-20460.
↑ Alkarkhi, A. F., Wasin, N. A. N. M., Alqaraghuli, A. A., Yusup, Y., Easa, A. M., & Huda, N. (2017). An investigation of food quality and oil stability indices of Muruku by cluster analysis and discriminant analysis. Int. J. Adv. Sci. Eng. Inf. Technol, 7(6), 2279-2285.
↑ Fitzpatrick, A. M., Teague, W. G., Meyers, D. A., Peters, S. P., Li, X., Li, H., ... & National Institutes of Health. (2011). Heterogeneity of severe asthma in childhood: confirmation by cluster analysis of children in the National Institutes of Health/National Heart, Lung, and Blood Institute Severe Asthma Research Program. Journal of allergy and clinical immunology, 127(2), 382-389. "To determine the strongest predictors of cluster assignment, stepwise discriminant analysis of the cluster variables was performed with the Fisher method..."

拎

Discriminant Analysis, IBM （英文），呢篇文有一步一步噉教埋點樣用 SPSS 嚟行 LDA。
Linear Discriminant Analysis in R Programming, GeeksForGeeks （英文），呢篇文教人點樣用 R 語言嚟做 LDA。

[3] Tharwat, A., Gaber, T., Ibrahim, A., & Hassanien, A. E. (2017) 嗰篇文 2.2 嗰 part 有詳解呢條式，原版英文係："m_i represents the projection of the mean of the i-th class and it is calculated as follows, m_i = W^T µ_i, where m is the projection (投射) of the total mean of all classes (所有類別嘅整體平均) and it is calculated as follows, m = WT µ, W represents the transformation matrix (變換矩陣) of LDA, µ_i (1 × M) represents the mean of the i-th class."

[4] 有關呢啲數學符號嘅意思，可以睇睇加總同集合。

[1] R. O. Duda, P. E. Hart, and D. G. Stork. Pattern classification. John Wiley & Sons, Second Edition, 2012.

[tharwat2017-2] 2.0 ^2.1 Tharwat, A., Gaber, T., Ibrahim, A., & Hassanien, A. E. (2017). Linear discriminant analysis: A detailed tutorial (PDF). AI communications, 30(2), 169-190，第一句就提到 dimensionality reduction 嘅概念。

[5] J. Ye, R. Janardan, and Q. Li. Two-dimensional linear discriminant analysis. In Proceedings of 17th Advances in Neural Information Processing Systems (NIPS), pages 1569-1576, 2004.

[6] J. Lu, K. N. Plataniotis, and A. N. Venetsanopoulos. Face recognition using lda-based algorithms. IEEE Transactions on Neural Networks, 14(1):195-200, 2003.

[7] Bilgili, B., & Ozkul, E. (2015). Brand awareness, brand personality, brand loyalty and consumer satisfaction relations in brand positioning strategies (A Torku brand sample). Journal of Global Strategic Management| Volume, 9(2), 10-20460.

[8] Alkarkhi, A. F., Wasin, N. A. N. M., Alqaraghuli, A. A., Yusup, Y., Easa, A. M., & Huda, N. (2017). An investigation of food quality and oil stability indices of Muruku by cluster analysis and discriminant analysis. Int. J. Adv. Sci. Eng. Inf. Technol, 7(6), 2279-2285.

[9] Fitzpatrick, A. M., Teague, W. G., Meyers, D. A., Peters, S. P., Li, X., Li, H., ... & National Institutes of Health. (2011). Heterogeneity of severe asthma in childhood: confirmation by cluster analysis of children in the National Institutes of Health/National Heart, Lung, and Blood Institute Severe Asthma Research Program. Journal of allergy and clinical immunology, 127(2), 382-389. "To determine the strongest predictors of cluster assignment, stepwise discriminant analysis of the cluster variables was performed with the Fisher method..."

[1]

[2]

[詳解 1]

[詳解 2]

[3]

[4]

[5]

[6]

[7]