空間

 唔好同太空搞亂。

空間（粵拼：hung1 gaan1）係哲學同科學嘅一個研究對象，佢好難落到一個定義。空間係咪可以度到都係一個爭論點。唔同科有唔同定義，不過多數都用操作定義，即係定義量度單位。

用嚟描述空間嘅3D座標系統

幾何概念

平面上面嘅一拃點；每粒點都可以想像成「塊平面」呢個集入面嘅一個元素。

幾何學係研究空間嘅數學子領域。「『空間』呢個概念要點定義」係一條可以幾撈絞嘅問題，不過喺最基本（歐幾里得幾何）上，空間可以用點、直線同埋平面等嘅概念想像。

0D：點

點係幾何學上嘅一個原始諗法：

• 簡化噉講，點可以定義做「喺空間裡面有確切位置、唔佔用空間嘅嘢」，冇長度同闊度；
• 技術性啲噉講，現代數學有咗集合論，而喺呢套理論框架下，點通常俾人定義做「一個集（空間）入面嘅其中一件元素」，例如想講一塊平面上面嘅一點，首先就會定義塊平面係

  $\mathbb {R} ^{2}=\{(a,b):a,b\in \mathbb {R} \}$，

塊平面上嘅一點 $p$ 就係 $\mathbb {R} ^{2}$ 入面嘅元素；用日常用語講嘅話，即係 $p$ 可以寫做 $(a,b)$，當中 $a$ 同 $b$ 都係實數（$\mathbb {R}$）。值得一提嘅係，點原則上係一個抽象化嘅概念，淨係存在喺人嘅想像之中：理論上嘅點係冇長度同闊度嘅，而當一個人攞支筆畫一粒肉眼睇得到嘅點嗰陣（好似下圖噉），嗰點查實經已有返咁上下長度同闊度，所以人先可以用肉眼睇得到，嚴格嚟講唔可以算係一點，頂嗮攏只可以算係攞嚟表示一點嘅符號。

點係幾何學最根基嘅諗頭－有咗點嘅概念，就有得定義同闡述第啲重要嘅幾何學概念同諗法，例如「是但兩點之間，都可以畫條獨一無二嘅線」呢條公理噉。

1D：直線

直線係幾何學想像中一種「冇闊度、有長度嘅嘢」，當中「直」係指「上面啲點均勻噉分佈嘅線」：

• 攞住點嘅概念，想像攞是但兩點 $A$ 同 $B$，喺 $A$ 同 $B$ 之間有無限咁多粒點，嗰啲點之間每對點之間嘅距離都係恆定嘅（$=0$）；
• 用集合論嘅角度嚟睇嘅話，一條線可以想像成由一大拃點組成嘅集－精確啲講，喺現代幾何學入面，直線通常俾人定義做「喺個線性空間入面，有某種線性關係嘅點集」；是但攞一粒點 $p$ 同一條線 $\ell$ 嚟睇，「$p$ 喺 $\ell$ 上面」或者「$p$ 唔喺 $\ell$ 上面」都會係有意義嘅句子－句嘢一係真一係假。
• 平面入面嘅直線有個性質，就係是但搵兩點，嗰兩點都可以用一條直線連接（睇返歐幾里得幾何嘅第一公理），而且喺所有「能夠連接兩點嘅線」之中直線係長度最短嘅；

好似下圖噉就係一條「線」－下圖條線實質上有闊度（如果唔係就唔會用肉眼睇得到），所以只係一個用嚟表示一條線嘅符號。

喺歐幾里得幾何入面，兩條直線之間可以有交點（intersection；一粒同時屬嗰兩條線嘅點），又可以有平行（parallel）嘅關係－如果話兩條線係平行嘅，意思係話無論將嗰兩線延長幾多都好，兩條線都唔會有交點。好似下圖噉，下圖有三條線 $t$、$r$ 同 $s$，當中 $t$ 同 $r$ 喺 ABCD 嗰點（頂點）相交，而 $t$ 同 $s$ 喺 EFGH 嗰點（都係頂點）相交，$r$ 同 $s$ 平行：

直線仲可以掕埋「曲線」嘅概念：曲線係一種幾何物體；同直線一樣，曲線可以想像成由兩點之間嘅點組成嘅集，不過曲線「可能係唔直嘅」嘅（好似下圖噉）；技術性啲噉講，曲線可以想像成直線嘅廣義化－「線」可以包嗮所有「由兩點之間嘅點組成嘅集」，而直線就計係線嘅一種，特指「上面啲點均勻噉分佈嘅線」。

2D：平面

喺歐幾里得幾何裏面，一塊平面係一塊 2D 而且冇曲率嘅幾何物體，有長度同闊度但冇高度，（最少理論上）可以向住任何方向無限噉延伸。如果用最常用嗰隻坐標系統嚟諗嘅話，平面同直線嘅分別可以想像成「要用幾多個數先可以描述一點嘅位置」（睇埋維度同坐標等嘅概念）－

• 如果要描述一點喺條線上面邊個位，淨係要用一個數，例如 $(x)$，所以係一維（1D）；
• 而如果要描述一點喺塊平面上面邊個位，就要用兩個數至得，例如 $(x,y)$，所以係二維（2D）；

下圖係互相成平行嘅三塊平面（想像三塊平面都冇高度－即係無限咁薄）：

歐幾里得研究嘅幾何好大部份都係喺平面入面發生嘅幾何（即係所謂嘅平面幾何），包括咗平面上面嘅三角形、圓形、平行線同角度呀噉。而根據呢套研究，平面有好多特別嘅性質：

• 是但攞兩塊唔同嘅平面，佢哋一係彼此成平行、一係就會係某條線嗰度相交；
• 是但攞一塊平面同一條線，條線一係同塊平面成平行、一係會喺某點同塊平面相交、再唔係就可能喺塊平面上面；
• 如果有兩條唔同嘅線，兩條都係同一塊平面成垂直（簡化講就係成 90° 角），噉兩條線實係平行嘅；
• 如果有兩塊平面都同某條線成垂直，噉兩塊平面實係成平行嘅；

... 呀噉。

兩塊相交兼成垂直嘅平面 兩塊相交兼成垂直嘅平面  線 同平面 成垂直。 線 $\ell$ 同平面 $A$ 成垂直。  線 同啲平面成垂直，啲平面彼此平行。 線 ${\text{S}}$ 同啲平面成垂直，啲平面彼此平行。

圓形係一種 2D 嘅形狀；用坐標諗嘅話，一個圓形條邊上面嘅每一點 $(x,y)$ 都會滿足以下條式－
$(x-a)^{2}+(y-b)^{2}=r^{2}$
當中 $(a,b)$ 係個圓心嘅坐標值，而 $r$ 係個圓形嘅半徑有幾長。

一去到 2D，就可以諗埋角嘅概念：是但攞一點（例如下圖嘅 $A$），由嗰點向住兩個方向（例如下圖嘅 $C_{1}$ 同 $C_{3}$）各射一條直線出去嘅話，兩條射線之間就會形成一隻角（下圖 $\alpha _{2}$），而角度就係一隻角可以有嘅特性，反映隻角「有幾大」；喺實際嘅幾何分析上，一隻角通常會用 $\angle$ 嘅符號嚟表示，下圖嘅 $\alpha _{2}$ 會寫做 $\angle C_{1}AC_{3}$ 噉嘅樣，而且會用噉嘅符號表示啲角嘅大細－$\angle ABC=90$ 表示「$\angle ABC$ 呢隻角係 90° 咁大」... 如此類推。

3D 或以上

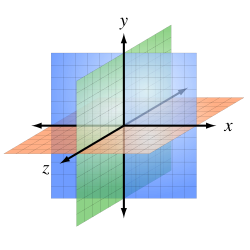
有咗點、直線、曲線、平面同角呢啲基本概念，研究者就可以對現實世界嘅空間做出基本嘅分析：3D 空間指笪空間入面嘅每個可能點都要有三個數 $(x,y,z)$，先可以講明佢喺邊個位－人類日常生活當中會接觸到嘅世界，就可以想像成一笪 3D 空間，有三條完全直嘅軸；响呢笪 3D 空間裏面，

• 每件物體都有長度、闊度同高度表示佢「掗咗幾多空間」，
• 每件物體都可以沿三條軸郁動－可以有前後左右上下一共六個方向；

一笪 3D 空間會有好多點，可以有直線、曲線同平面，而線之間或者平面之間（或者線同平面之間）可以有角度。

一個球體；當中 係個球體嘅半徑。 一個球體；當中 $r$ 係個球體嘅半徑。  一個立方體；定義上，一個立方體每條邊都一樣咁長，而且是但搵其中兩條邊睇，嗰兩條邊都成直角。 一個立方體；定義上，一個立方體每條邊都一樣咁長，而且是但搵其中兩條邊睇，嗰兩條邊都成直角。  3D 空間嘅旋轉動畫；喺一笪 3D 空間入面，一點嘅位置可以表示做 噉嘅樣，當中每個數表示嗰點沿其中一條軸嘅位。 3D 空間嘅旋轉動畫；喺一笪 3D 空間入面，一點嘅位置可以表示做 $(x,y,z)$ 噉嘅樣，當中每個數表示嗰點沿其中一條軸嘅位。

對 3D 或以上維度嘅空間嘅分析好有用。幾何學家會用數學證明嘅方法，探究點、線同埋空間有咩特性，而第啲領域嘅工作者就可以攞住呢啲知識去做嘢：喺廿一世紀初嘅多數工程學應用上，分析空間嘅特性可以齋靠「將空間想像成笪 3D 空間，而且每個位置都可以用實數坐標表示」就搞得掂－呢種分析可以攞嚟分析交通工具（汽車等嘅嘢郁動，就係改變喺空間入面嘅位置）同建築物（一棟建築物會有長度、闊度同高度）等工程學上會想分析嘅嘢；古典物理學上嘅分析可以齋靠 3D 就搞得掂，而進階嘅物理學－例如廣義相對論－仲會用到多過三個維度嚟描述時空。

睇埋

• 時間
• 視覺藝術，本質上就係「喺空間當中編排色彩」嘅藝術