人工神經網絡
人工神經網絡(英文:artificial neural network,ANN,可作粵拼:ei1 en1 en1)係一類數學模型,特徵係設計上模仿生物神經網絡(即係動物嘅中樞神經系統,尤其係個腦)嘅結構同功能:例如一隻靈長目動物嘅腦閒閒哋有
一個 ANN 由大量人工神經細胞組成。用電腦程式整神經網絡嗰陣時,研究者通常會每粒人工神經細胞都同佢設返個數值表示佢啟動程度有幾高[6],而每粒神經細胞嘅啟動程度數值都有條式計,條式包括喺佢之前嗰啲神經細胞嘅啟動程度。啲函數裏面嘅參數可以變化,而如果個神經網絡程式令佢識得靠經驗嚟調整呢啲參數嘅話,個神經網絡就會具有學習能力[7][8]。即係例如個程式每粒細胞有條類似噉嘅算式:
- ;(啟動函數)
代表粒手上粒細胞嘅啟動程度, 代表前排神經細胞當中第 粒嘅啟動程度,而 就係細胞 嘅權重—指佢有幾影響得到 。噉每當一粒人工神經細胞啟動嗰陣,會帶起佢後面啲細胞跟住啟動-似十足生物神經網絡噉[7][9]。
到咗廿一世紀初,ANN 經已俾科學界廣泛噉用落各種問題度。喺應用上,事實證實 ANN 能夠處理機械視覺同語音識別等傳統電腦程式搞唔掂嘅問題[10][11];而理論性質認知科學亦有聯結主義嘅諗頭,主張心靈可以用 ANN 技術嚟模擬[12]。
人工智能史嗰度有詳細啲噉講人工神經網絡呢樣嘢嘅歷史。
基本諗頭 編輯
人工神經網絡最基本嘅諗頭係
| 「 | 要用人工方法模仿動物神經細胞嘅功能。
|
」 |
一粒神經細胞[歐 1]受到某啲特定刺激嗰陣,會用電或者化學方式向第啲神經細胞傳出訊號,然後同呢粒神經細胞相連嗰啲神經細胞會受到佢訊號刺激,跟住又會各自射新嘅訊號-令到資訊就會擴散開去,傳去神經系統唔同部份[13]。
例如隻眼塊視網膜上面嗰啲感光神經細胞噉,呢啲細胞受光刺激嗰時,會傳訊號去同佢哋相連嘅神經細胞嗰度,而呢一串神經細胞一路連到上腦,所以喺每一點時間,對眼嗰啲感光細胞都會係噉受光刺激並且射訊號,啲訊號會一路傳上去個腦嘅視覺相關區域,個腦處理收到嘅資訊—例如係有幾多粒感光神經細胞喺度射訊號、或者射訊號嘅係喺眼邊忽嘅感光細胞... 等,就可以判斷對眼睇到啲乜[14][15]。
呢種訊號傳遞過程,就係人工神經網絡技術想模擬嘅嘢[16]。
網絡組成 編輯
細胞 編輯
一粒人工神經細胞係一嚿人造物體,會好似動物神經細胞噉收訊號、並且按照收到嘅訊號改變自己嘅內在狀態,然後再按照自己嘅內在狀態,決定係咪要射新訊號以及要射點樣嘅新訊號-喺原理上同動物嘅神經細胞極相似[註 1][17]。當一大拃人工神經細胞互相連繫住,就會形成一個人工神經網絡,每當研究者俾某啲 input 值落去其中一啲細胞嗰陣,佢哋就會帶動其他人工神經細胞啟動,最後每粒人工神經細胞都會達致最後嘅啟動值。噉亦表示,個網絡可以有 output 畀到出嚟。實證研究表明,一個人工神經網絡嘅 output 值同 input 值會成特定嘅關係,因而可以攞嚟做一啲有用嘅運算(下面詳細講)[16][18]。
一粒典型人工神經細胞嘅結構如下[16]:
- 至 係各個 input 嘅數值,啲 input 可以係嚟自外界嘅,但又嚟自同一個網絡入面嘅第啲神經細胞都得。
- 至 係每個 input 嘅權重[歐 3],代表嗰個 input 對手上呢粒神經細胞嘅啟動程度有幾大影響力。
- 指偏向[歐 4],即係嗰粒神經細胞本身喺啟動上有乜傾向,例如如果有某粒神經細胞嘅 係正數而且數值大,佢就會傾向無論 input 係幾多都有強烈啟動[19][20]。
- (以下簡稱 )指粒神經細胞嘅啟動程度[歐 5],呢個數值由上面嗰柞因素話事,個函數如下:
- 指粒細胞喺時間點 嘅啟動程度,
- 指粒細胞喺時間點 嘅啟動程度,
- 而 指喺時間點 嗰柞輸入嘅數值。呢條式表示, 嘅值取決於 、 同埋 呢三個數值。
- 好多人工神經細胞嘅啟動函數仲會包含 嘅數值。呢個係所謂嘅門檻值[歐 6]:一粒典型嘅動物神經細胞,一定要受到嘅刺激有返咁上下勁,先至會射訊號;如果佢受嘅刺激數值過唔到門檻值,佢就咩訊號都唔射;為咗要更加貼近動物神經細胞,好多研究人員設計人工神經網絡嗰時都會特登同每粒細胞俾返個門檻值佢,令各粒人工神經細胞好似動物神經細胞噉,收到嘅 input 唔過門檻值就完全唔射訊號。
- 係粒人工神經細胞嘅輸出數值。
- 係 同埋 之間嗰個函數,可以有多個款,但 好多時會係一個恆等函數[歐 7]-即係話 數值好多時同 一樣。
傳遞函數 編輯
喺數學上,一粒普通嘅人工神經細胞成個傳遞函數[歐 8]可以簡化噉用以下呢條式表達:
- 係權重向量[歐 9],即係指包括嗮所有權重在內嘅一個向量[註 2]。
- 係輸入向量[歐 10],同理係指包括嗮所有 input 在內嘅一個向量。
- 係粒人工神經細胞嘅 output,係一個純量[歐 11]。
以上呢個函數所講嘅嘢用日常用語表達係噉嘅[16]:
| 「 | 粒人工神經細胞嘅 output 值取決於佢收到嘅 input 值、啲權重同埋佢嘅偏向值。
|
」 |
上述呢個例子係一個線性函數[歐 12](即係如果將 同是但一個 畫幅圖,會出一條直線),不過喺實際應用上,人工神經細胞嘅傳遞函數仲有得用
網絡結構 編輯
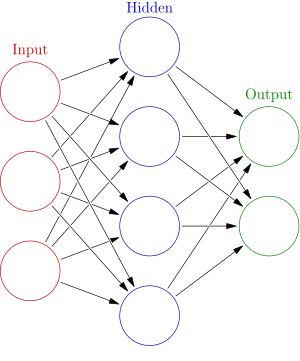
當多粒人工神經細胞連埋一齊,就會組成一個人工神經網絡。喺實際使用上,設計者一般會用電腦程式整人工神經網絡,叫個程式開始嗰陣粒粒細胞都設個數代表佢嘅啟動程度,再設啲數代表細胞之間嘅連結權重。網絡多數會用多層結構-同一層嘅細胞唔會影響彼此嘅啟動程度,粒粒嘅啟動程度都會受前一層嘅細胞影響。例如常見嘅多層前饋網絡[歐 14]可以想像成以下噉嘅樣[22][23]:
幅圖入面嘅每一個圓圈都代表咗一粒人工神經細胞,箭咀表示箭咀前嗰粒細胞嘅啟動能夠影響箭咀後嗰粒細胞嘅啟動(箭咀後細胞嘅啟動 箭咀前細胞嘅啟動 )。呢個網絡由三大層組成,分別係[22]:
- 輸入層[歐 15]嘅細胞負責由外界嗰度攞資訊-佢哋嘅啟動程度主要由呢啲外界資訊話事。
- 隱藏層[歐 16]係 input 層同 output 層之間嘅一排排人工神經細胞,得一層或者有好多層都得,一粒隱藏層入面嘅細胞嘅啟動程度通常都係取決於佢打前嗰層嗰啲細胞。一般嚟講,隱藏層愈多細胞,個網絡嘅就愈會有顯著嘅非線性[歐 17],但表現唔一定會愈好[24]。喺實際應用上,研究者整神經網絡嗰陣,會設每浸隱藏層嘅細胞數目做 input 層嘅 1.2 至 1.5 倍。
- 輸出層[歐 18],呢層嗰啲細胞嘅啟動程度取決於佢哋之前嗰層嘅細胞,負責俾出成個神經網絡嘅運算結果。
亦都有一啲人工神經網絡係冇隱藏層嘅。呢啲網絡浸 output 層嘅啟動程度數值會直接噉由 input 層決定,即係話佢哋結構如下:
當中左手邊黑點代表 input 層嘅細胞。呢種冇隱藏層嘅神經網絡有個大缺點,佢哋模擬嘅 input-output 關係唔能夠太複雜,一旦個設計者需要段 input-output 關係唔係簡單線性嗰陣,單層人工神經網絡往往就會搞唔掂[25][26]。
前饋定遞迴 編輯
按照結構嚟分類嘅話,神經網絡有得分做好多種,以下呢兩大種最常見[27]:
- 前饋神經網絡[歐 19],指訊號淨係由 input 到 output 一個方向流動嘅神經網絡-冇任何細胞能夠影響自己前排嗰啲細胞,好似上面嗰幾幅圖描述嘅噉。
- 遞迴神經網絡[歐 20],指訊號會喺個神經網絡內「遞迴」,即係話個網絡有一啲細胞有能力影響佢哋之前嗰幾層嘅細胞嘅啟動程度[28]。因為佢哋呢種結構特徵,佢哋識得處理喺時間上前後倚賴嘅資訊。例如係自然語言[歐 21]噉[29]:一個人講嘢嗰陣,句子嘅第二隻字會影響到第一隻字嘅意思,例如粵文家吓同家庭嘅意思就唔同嗮,所以要分析時間點 聽到嗰隻字,梗要考慮埋打前時間點聽到嘅字先得-遞迴神經網絡就能夠做到呢一點。事實係喺廿一世紀初,已經有研究者成功噉用遞迴神經網絡嚟教電腦處理自然語言[29]。例如以下呢幅圖噉:
喺呢個網絡當中,一粒細胞可以影響佢自己喺下一點時間嘅啟動程度。所以個網絡係一個簡單嘅無隱藏層遞迴網絡。
網絡學習 編輯
學習法則[歐 22]係指一個神經網絡有嘅一拃法則,負責講明個網絡啲參數要點變化。
一個神經網絡收到一個 input 嗰陣會計一個 output 出嚟,但係呢個 output 唔一定係正確嘅,可能會同正確嘅結果有所出入[註 3]。所以如果要用神經網絡計出正確結果,好多時就要靠好似學習噉嘅過程[30]:例如喺監督式學習當中,個研究者可以走去搵數據返嚟-呢柞數據就係所謂嘅訓練集[歐 23];訓練集會包括一連串嘅 input 個案,而每個個案都有一個已知嘅正確 output 值;跟住研究者就可以將訓練集嘅數據入落去神經網絡程式度,等部電腦自動噉計每一個個案入面,個神經網絡俾出嚟嘅 output 同正確 output 值爭幾遠,然後啲事先編好嘅學習法則,就會按照呢啲差異值計吓例如權重要點變,先可以令個網絡俾出更準嘅答案。如是者,個神經網絡運算咗大量個案之後,佢啲權重參數值就會有所改變,(喺理想情況當中)變到更加能夠計到正確答案[16]。睇埋通用近似定理。
喺呢個過程裏面,個研究者會想令以下條方程式入面嗰個殘差平方和 有咁細得咁細[31][32]:
- 係個訓練集入面嘅個案數量;
- 係第 個個案入面嗰個輸入;
- 係個神經網絡用 做輸入嗰陣俾出嚟嘅輸出;而
- 係第 個個案入面嗰個正確輸出;所以
- 呢個數值反映咗攞個神經網絡嚟計嘢嗰陣嘅平均誤差。
反向傳播 編輯
反向傳播算法[歐 25]係一套用嚟計權重值要點調整嘅方法。個網絡俾出運算結果之後,就可以計吓個結果同正確數值爭幾遠[33][34],例如確率勾配降下法[歐 26]噉,就會用以下呢條算式嚟計出每個權重值要點變[35]:
- ;當中
如果一個以電腦程式寫嘅神經網絡跟呢條式嚟行,佢計完每一個個案之後,都會計出佢裏面嘅權重值要點變,並且將呢件「每個權重應該要點變」嘅資訊傳返去個網絡嗰度(所以就叫反向傳播)。每次有個權重值改變嗰陣,佢嘅改變幅度會同誤差值有一定嘅關係,而且佢對個 output 嘅參與愈大,佢嘅改變幅度會愈大[38]-個網絡會一路計個案一路變,變到誤差值愈嚟愈接近 0 為止[22][39]。而除咗確率勾配降下法之外,反向傳播仲有好多其他方法做,詳情可以睇最佳化[歐 28]相關嘅課題[40][41]。
用反向傳播算法幫神經網絡學習嘅演算法如下[42][43][44]:
- 第一步:傳播
- 由數據度攞一個個案,按照個網絡嘅權重同個案嘅 input 值計個網絡會俾乜嘢 output 值(計 );
- 計吓誤差係幾多(計 同 );
- 用條式計吓每個權重數值應該要變幾多(計 )。
- 第二步:更新權重值
- 每個權重值,佢都會由條式嗰度有一個梯度值[歐 29];
- 每個權重值嘅改變幅度等如個梯度值乘以 -如果 係 0,噉個網絡永遠都唔會變,而如果 數值大,噉個網絡會變化得好快,所以 掌管個網絡「學嘢學得幾快」;
- 將呢拃值「反向傳播」返去個網絡度,將每個權重值變成佢嘅新數值(實際更新 值);
- 重複以上步驟,理想嘅係直至誤差值變成 0 為止,或者係變到一個接受得到嘅程度。不過都可以睇埋過適嘅概念。
如果想搵實際寫神經網絡同教啲網絡學習嘅源碼,網上周圍都有。
批量式 編輯
要用反向傳播算法訓練神經網絡,可以用所謂嘅批量式訓練[歐 30]。喺一個用批量式訓練學嘢嘅神經網絡入面,源碼會講定一個批量嘥
設定 maxEpochs 嘅數值 將拃數據睇 maxEpochs 噉多次 同每個個案,做... 計啲權重要變幾多。 累積權重值變幅,而唔係即刻改變啲權重值。 Run 嗮所有個案之後,先 update 柞權重值;喺呢段碼入面,b = 個案數量
批量式訓練有個好處係,用呢種做法表示每次權重更新都考慮嗮成個批量入面嘅趨勢,而唔係淨係考慮單一個案,所以畀人指係可以令神經網絡學起嘢上嚟更穩定[45]。
學習率 編輯
學習率[歐 32]( )係神經網絡入面好緊要嘅參數。每次更新啲權重之前,都要有條式計每個權重變幾多,而個變幅往往會乘以個學習率—即係話學習率掌管住個網絡「學嘢學得有幾快」,如果學習率係 0 個網絡啲權重值就永遠都唔會變,而學習率數值大,個網絡就會變得好快。
之但係「學得快」唔一定係一件好事[47]:學習率快就表示每次更新權重嗰陣,每個權重變幅都會偏大,呢種情況好多時會搞到權重變嗰陣「郁到過咗龍」-假想有個權重家陣數值係 0.7,而佢個理想值係 0.65,但因為個網絡學習率勁得滯,搞到權重更新嗰陣佢個數值唔係變成理想嘅 0.65,而係變成 0.6;同時另一方面,學習率低得滯又會搞到個網絡學嘢好慢。因為噉,對神經網絡嘅研究就成日講到「學習率要設做幾多先算理想」呢條問題[48][49]。
喺最原始嘅神經網絡當中,學習率係常數,但廿一世紀初嘅研究有嘗試將學習率設做可以變化嘅數值[50][51]。其中一個比較簡單嘅方法係運用所謂嘅動量[歐 33][註 4]:喺神經網絡研究上,動量建基於一個諗頭-如果喺之前幾個個案入面,權重都係要跌嘅話,噉呢個權重喺下一個個案當中好可能都係要數值跌,而同理如果個權重喺之前幾個個案入面都係要升嘅話,噉佢好有可能喺下一個個案都係要升[52]。
噉即係話喺一個原始嘅神經網絡裏面,一個權重嘅改變幅度如下[50]:
- 當中 係權重改變幅度, 係學習率, 係梯度值。而喺用動量嘅情況下,權重變幅條式如下[50]:
係一個常數,掌控「動量衰退得有幾快」,而 喺之前嗰個個案入面嘅權重變幅-即係話喺呢個情況下,當個權重(例如)喺之前嗰一個個案係下降咗嗰陣,佢喺今個個案下降起上嚟會下降得更勁,而上升起上嚟會上升得冇咁快(呢點有少少似物理學上嘅動量)。調較 嘅數值可以左右「之前嘅權重變幅」對「而家嘅權重變幅」有幾大影響力[50]。
學習範式 編輯
一個神經網絡可以隨住經驗變得更加有能力做準確嘅預測-曉好似動物噉樣學習。所以神經網絡技術對機械學習嚟講至關重要,而要訓練一個神經網絡學嘢,主要有三大學習範式:監督式學習、非監督式學習同埋強化學習[53][54]。
監督式 編輯
監督式學習[歐 34]會搵一柞例子個案返嚟,將每個個案嘅 input 入落去個網絡度等佢計個 output 出嚟,跟手再計返誤差值同埋用誤差值計個網絡啲權重要點改。經過一輪訓練,個網絡對訓練集數據嘅計算結果個誤差值可以接受,就將未見過嘅測試集數據挃入隻網絡進行預測,又得到泛化誤差值。若果個誤差值都可以接受得到,噉意味呢個網絡模型實現咗泛化,可以作為結果呈現;唔係就要調整權重、返去重新訓練。用數學行話講嘅話,即係要搵出一柞已知嘅例子,有若干對輸入( )同正確輸出( ), ,並且由可容許嘅函數當中搵返個同啲例子最吻合嘅函數 出嚟[53]。喺呢種學習之下,個神經網絡會由個研究者嗰度收到一柞訓練數據俾佢學、入邊有題同埋答案,好似有個老師噉-所以就叫監督式學習[53][55]。
用監督式學習可以訓練神經網絡做好多嘢,好似係圖形辨識[歐 35][56]同埋迴歸分析[歐 36] [57]呀噉。舉例說明,家吓有個研究員想訓練一個神經網絡分辨一個病人係咪有肺癌[58],用嚟幫啲醫生手做檢查;佢可以
- 去問醫院同醫學院等嘅單位借有關肺癌病人嘅數據,呢柞數據要包括咗每個病人嘅檢查結果( )以及佢係咪真係有肺癌( )等嘅資訊;
- 跟手個研究員就會逐個逐個將啲病人個案嘅檢查結果同 X 光片嗰柞數字入落去個神經網絡嘅輸入層嗰度,啲隱藏層會計吓啲輸入嘅數據,而個輸出層就會係是但一個二元[歐 37]嘅輸出-有肺癌(用 1 代表)同冇肺癌(用 0 代表)。
- 初頭嗰陣,個網絡實會犯好多錯,但係用呢柞數據訓練到咁上下之後,個網絡會根據佢啲學習法則改變佢啲權重,順利嘅話啲誤差會變到愈嚟愈細[59];而最後如果個誤差細到去一個可以接受嘅水平嘅話,醫生就有可能會有興趣用呢個神經網絡幫佢哋手檢查肺癌。
事實係,喺醫學上經已有唔少醫護人員會用神經網絡幫手做診斷,有研究甚至發現,用神經網絡嚟做診斷有陣時仲準過用人手做[60]。
非監督式 編輯
喺非監督式學習[歐 38]當中,個研究者會有一柞數據 俾個神經網絡處理,但係同監督式學習唔同嘅係,個研究者唔會明確噉話俾個神經網絡知佢做嘅預測係啱定錯-所以就嗌做非監督式學習[61][62]。
非監督式學習一個常見用途係攞嚟做聚類分析[歐 39]。舉例說明,家吓有個生態學家想研究吓一個區域入面嗰啲樹傾向聚集喺啲乜嘢位置,佢可以坐直昇機或者用人造衛星影啲相返嚟,再記錄嗮嗰個區域入面每樖樹生喺邊個位(呢個過程會嘥唔少時間),會得出一個數據庫,記錄嗮每樖樹喺 X 軸同 Y 軸嗰度嘅坐標。跟手佢就可能會想睇吓啲樹會唔會傾向聚集喺個區域入面嘅某啲位置(呢啲資訊可能有助佢保育一啲靠樹生存嘅動物)。如果有某一柞嘅樹彼此之間距離近,又同佢哋以外嘅樹距離遠,噉就可以話佢係「聚埋一羣」,而聚類分析就正係用嚟分析一柞個案入面會唔會有幾羣個體係「彼此之間距離近,同羣以外嘅個體距離遠」嘅[63][64]。
喺呢次研究入面,個生態學家唔會事先知道啲樹要點分羣,所以用唔到監督式學習[62],但係佢可以運用非監督式學習嚟整一個神經網絡幫佢手做呢個聚類分析。一個簡單嘅可能做法係好似以下噉:將浸輸入層設做樖樹嘅坐標,等啲隱藏層用每一樖樹嘅數據逐個逐個計吓,而浸輸出層就有例如 5 粒人工神經細胞,喺每樖樹嘅運算之後都會有一粒輸出層神經細胞嘅啟動程度係大過其他嘅-所以個生態學家就可以按「喺將嗰樖樹嘅數據入咗落去個神經網絡度之後,邊粒輸出層神經細胞嘅啟動程度最大」為準則將啲樹分做聚類,而且佢仲有得按照分類結果分得好唔好,嚟計吓使唔使改變吓個神經網絡嗰啲參數-個神經網絡喺度進行學習。除咗噉,電腦科學界仲有第啲更加精良嘅演算法嚟做非監督式學習[62][64]。
強化學習 編輯
強化學習[歐 40]係機械學習一種,喺機械人設計上好有用。喺神經網絡強化學習嘅過程裏面,研究者唔會有個數據庫 俾個神經網絡睇同跟住學,而係俾個神經網絡係噉同佢周圍嘅環境互動:喺每一個時間點 ,個神經網絡[歐 41]會產生一個用輸出嘅數字表示嘅動作[歐 42],例如用 0 代表企喺度唔郁同 1 代表向前行呀噉),而跟住佢周圍個環境[歐 43]會俾返一啲 feedback-簡單啲講就係話返俾個神經網絡聽佢個動作係咪一個好嘅決定,例如個地下有個窿,向前行會跌得好痛,然後個網絡會有方法[歐 44]知道呢個結果。個網絡跟住就會根據呢個 feedback 計吓,睇吓要點樣改佢嗰啲參數,先可以令到下次佢做行動嗰陣得到正面回應嘅機率高啲-上述呢個例子就有可能可以攞嚟教機械人行路[65][66][67]。
人工神經網絡強化學習嘅過程大致可以想像成噉[68][69]:
- 個神經網絡俾出一個輸出, ;
- 個環境會根據佢嘅內部運作法則決定回輸, ,係乜( 係現時狀態,而 係下一個狀態);
- 個神經網絡會根據 決定係咪要修改自己內部嘅參數同埋(如果要)要點改;
- 返去步驟 1。
個神經網絡內部要有一個演算法,個演算法要用 做輸入,然後輸出「內部參數要變幾多」。
Q-學習 編輯
Q-學習[歐 45]係強化學習上成日用嘅一種演算法,用 Q-學習嘅人工神經網絡會儲住一個數據庫,個數據庫包含咗一大柞「狀態-行動」嘅配對,每當有個行動喺某個狀態之下引致正面結果嗰陣,相應嘅狀態-行動配對嘅數值會上升,反之就下降-而當個神經網絡撞到類似狀態嗰陣,就可以靠「邊個行動同呢個狀態嘅配對數值最大」做準則決定採取乜嘢行動。Q-學習嘅核心係以下嘅更新算式[68][70]:
- ,當中
- 係狀態 同行動 之間嘅配對值;
- 係學習率;
- 係環境所俾嘅回輸,數值視乎 等因素而定。
- 呢條式表達嘅係,喺每一個時間點, 都有可能改變數值,而佢新數值由「佢之前個數值」同「環境所俾嘅回輸」話事,學習率就主宰咗「環境所俾嘅回輸」對佢有幾大影響力。
一個簡單-得兩個行動同兩個狀態-嘅 Q-學習神經網絡嘅演算法例子大致上如下(個網絡可以想像成有兩層,每層兩粒神經細胞)[68]:
- 初始化,將行動 1 粒神經細胞嘅權重, 同 (兩個權重分別代表嗰粒細胞同輸入層嗰兩粒細胞嘅連繫),設做隨機揀嘅數值,而行動 2 嘅相應神經細胞, 同 ,設做同一數值,以是但一個狀態開始系統模擬,「發生咗幾多次狀態改變」( )設做 0,將 嘅最大值( )設做一個大嘅數值。
- 係現時狀態, 就係下一個狀態。
- 評估每個 Q-因素[歐 46](狀態-行動配對嘅數值)。
- 更新啲權重,等下次再撞到 噉嘅狀態嗰陣,個網絡比較有機會作出能夠帶嚟回報嘅行動。
- 將 數值提升 1,除非 大過或者等如 ,返去步驟 2。
進階變種 編輯
學界有好多進階嘅神經網絡類型。呢啲網絡類型複雜過普通嘅前饋同遞迴網絡,好多時每種都係專門攞嚟處理某啲特定類型嘅問題嘅,好似係[71][72][73]:
圖像處理 編輯
人工神經網絡可以攞嚟幫電腦處理傳統演算法好難搞得掂嘅圖像。想像以下一個噉嘅神經網絡:佢係一個卷積神經網絡[歐 47],輸入層有若干粒細胞,若干浸隱藏層,同一浸輸出層;輸入層每粒細胞代表咗一個像素(幅圖片上面嘅某一個點),第一浸隱藏層就每粒細胞相應輸入層嘅某一橛仔-例如第一粒隱藏層細胞負責處理輸入層最左上角嗰 3 x 3 粒像素大嘅一橛仔(令到個網絡能夠處理啲解像度高嘅圖像),而最後輸出層有 10 粒細胞,每一粒輸出層細胞代表咗一個類別;個神經網絡有個演算法能夠由一幅圖片嗰度讀取輸入,所以每當佢讀到一幅圖片嗰陣,佢嘅神經細胞會跟住輸入層嘅啟動,最後輸出層嘅規律就可能提供到「幅圖屬於邊個類別」嘅資訊[74][75][76]。
喺電腦入面,一幅圖片可以用數字代表:一幅圖片由好多粒細點(像素)組成,每粒細點都有特定嘅色水;用三原色模式想像嘅話,任何色水都可以由紅、綠、同藍呢三隻原色砌出嚟,所以一個點嘅色水可以用 噉嘅陣列代表-當中 表示嗰一點嘅紅色量, 代表嗰點嘅綠色量,而 代表嗰點嘅藍色量,而一幅圖片喺部電腦內部可以用類似噉嘅陣列代表[74][77][78]:
- ,表示第一個點有 207 個單位咁多嘅紅、229 咁多個單位嘅綠、同 78 個單位咁多嘅藍,如此類推。
一個可以攞嚟將圖片分類嘅卷積神經網絡演算法(監督式學習)大致上如下[79][80]:
- 指定「有啲乜嘢類別」同埋啲輸入嘅圖片有幾多像素等嘅資訊;
- 由目標位置嗰度讀取圖片數據,得到每幅圖片嘅相應陣列,而且每幅圖片都要有個已知嘅類別;
- 做一啲事前處理[歐 48],等啲圖片方便由神經網絡處理;
- 建立一個卷積神經網絡,輸入層嘅細胞係圖片每粒像素嘅色水,而輸出層就係幅圖片「屬乜嘢類別」;
- 重複噉做監督式學習嘅基本過程(俾個網絡計出佢嘅答案,將佢嘅答案同正確答案相比,再按結果更改柞權重)。
最後如果順利嘅話,呢個神經網絡就會曉分一幅圖片到底係(例如)屬於 A 類定 B 類,即係例如分啲相係影緊貓定係影緊狗。
深度學習 編輯
喺廿一世紀嘅社會,互聯網嘅發展令到資訊嘅傳播變得好快,極大量嘅數據喺互聯網上流動,呢啲數據可以好有用,但係因為量大,所以用傳統嘅數據分析法好難處理,而大數據[歐 49]就係一門廿一世紀初嘅新興領域,專門研究點樣做自動化嘅數據分析同埋用呢啲分析方法由大量數據當中提取有用資訊,而人工神經網絡-尤其係深度信念網絡[歐 50]-就係大數據成日用嘅一種工具[81][82]。
深度信念網絡結構係噉嘅:一個深度信念網絡由多個受限玻茲曼機[歐 51]再加一個前饋神經網絡組成;一個 RBM 得一浸隱藏層,而隱藏層細胞之間冇任何相互連繫,但曉將佢哋嘅啟動傳返去輸入層嗰度;一個受緊訓練嘅深度信念網絡會以第一層 RBM 嘅隱藏層細胞做第二層嗰個 RBM 嘅輸入,再用演算法做學習嘅過程[83]。
一個深度信念網絡嘅演算法大致上如下[84]:
- 初始化-指定好啲參數同埋隨機設定權重值等等;
- 按照輸入層細胞嘅啟動同權重,計隱藏層細胞嘅啟動程度;
- 按照隱藏層細胞嘅啟動同權重,計輸入層細胞嘅啟動程度;
- 按重構誤差更新權重;
- 重複上述工序,直至誤差細過某個值為止。
喺一個 RBM 完成學習之後,個程式會「疊」另一個 RBM 喺上面-攞之前嗰個 RBM 嘅隱藏層做新嗰個 RBM 嘅輸入層,再重複上面嘅步驟,直至成個深度信念網絡有若干層 RBM 為止[85]。研究表明咗,深度信念網絡能夠有效噉處理一啲冇事先標籤好嘅數據-例如係喺互聯網上流動、冇人幫手事先執靚嘅數據噉[86]。
長短期記憶 編輯
長短期記憶[歐 52]係一種能夠記住長期記憶嘅遞迴神經網絡:一般嘅遞迴網絡曉處理連串性嘅資訊,例如係用自然語言寫嘅句子噉,但現實世界嘅解難好多時都要求一個個體能夠睇得出時間上差距大嘅因同果,例如要完全了解一個故仔嘅結局,可能要諗返起故仔開頭嘅情節。事實證明咗,普通嘅遞迴神經網絡好多時都難以應付呢啲問題[87]。
LSTM 網絡特徵係內置一啲門控神經細胞[歐 53],呢啲特殊嘅人工神經細胞有門[歐 54],曉決定要儲起乜嘢資訊同埋幾時讀取、寫入、或者刪除資訊:喺 LSTM 網絡嘅碼當中,會有演算法幫門控細胞決定幾時要改變自身嘅啟動程度;相比之下,一般嘅遞迴神經網絡冇能力控制現存嘅過去資訊會唔會喺新資訊嚟到嗰陣被替換。呢個特點令到 LSTM 網絡有能力儲資訊儲好耐,而且有能力由輸入嘅數值當中搵出時間上相距不定嘅因同果[87][88]。
一粒 LSTM 嘅人工神經細胞除咗主細胞( )之外仲有幾個元件[87]:
呢三道門當中每一道都可以當係一粒子細胞噉嚟睇,有各自嘅啟動程度值,會受到第啲人工神經細胞影響,決定自身嘅啟動程度,再按自身嘅啟動程度睇吓係咪要「做嘢」。輸出門「做嘢」嘅話會左右甚至封鎖粒細胞嘅輸出,輸入門「做嘢」嘅話會左右甚至封鎖粒細胞嘅輸入,而遺忘門「做嘢」嗰陣就可以完全刪除粒主細胞入面嘅資訊-即係重設粒主細胞嘅啟動值或者權重等[89][90]。研究表明咗,LSTM 網絡可以用嚟教電腦做一啲要求長期記憶嘅作業,例如係閱讀理解呀噉[87][91]。
批評 編輯
「黑盒」 編輯
有好多神經網絡相關領域嘅學者批評神經網絡係「黑盒」[歐 58][92]。
人類用個腦諗完嘢解決完問題之後,曉將自己嘅思考過程口頭報告返出嚟,但係一個神經網絡唔會識做呢樣嘢,唔會話到俾研究者聽佢經過啲乜嘢思考過程先能夠達到佢所俾嘅輸出。所以有人將神經網絡比喻做一個黑盒-就算佢嘅輸出係準確嘅都好,個研究者都淨係知個神經網絡嘅輸入同輸出,冇辦法知道當中嘅思考過程。即係話對於「個神經網絡俾嘅答案點解係啱」呢條問題,目前唯一嘅答覆係「因為一部醒過人類嘅系統俾咗個答案出嚟」,雖然呢點唔損害神經網絡喺實用上預測現象嘅能力,但噉表示神經網絡嘅可解釋度[歐 59]低得好交關,好多學者都覺得難以接受[93][94][95]。
因為噉,有好多科學家都致力研究點樣先可以拆解一個經歷咗訓練、做緊準確預測嘅神經網絡[92][96]。
理論特性 編輯
雖然話人工神經網絡成個諗頭係建基於生物神經網絡嘅,但查實佢哋喺好多地方都同生物神經網絡好唔同,例如[17]:
- 拓撲特徵:一個普通嘅人工神經網絡會分開做若干層,同一層嘅人工神經細胞彼此之間冇任何連繫,而且做起運算上嚟好多時都係逐層逐層噉做嘅,但生物嘅神經網絡通常都冇明顯分層,而且做起運算上嚟係成個網絡各部份同時間噉做嘅。有關唔分層嘅神經網絡,可以睇霍菲特網絡[歐 60][17]。
- 速度:喺生物神經網絡當中,訊號嘅速度唔淨只影響個網絡嘅運算速度,仲可以影響所傳送嘅資訊嘅內容,例如係人類嘅眼噉,眼嘅感光神經細胞會向個腦塊視覺皮層傳訊號,話俾個腦知睇到啲乜,而神經科學上嘅研究表明咗,一粒感光神經細胞射訊號嘅頻率係用嚟俾個腦知道光嘅強度嘅(詳情可以睇神經編碼);相比之下,一個普通嘅人工神經網絡之中訊號嘅速度同頻率淨係會影響個網絡嘅運算速度[98]。
- 容錯:喺生物神經網絡當中,一份資訊係儲多咗幾份嘅,所以個網絡能夠容許訊號傳播上嘅出錯,就算傳訊號嘅過程裏面個訊號走咗少少樣,都唔會造成記憶損失,而且生物神經網絡冇「中央」部份,就算個腦某部份受損,個腦嘅第啲部份好多時都有能力自己改變等自己可以做埋受損嗰部份本嚟做嘅工作。相比之下,人工神經網絡一般冇呢啲能力[99]。
- 反向傳播:生物神經網絡並冇任何類似反向傳播嘅機制[100]。
因為呢啲原因,科學界普遍質疑到底人工神經網絡可唔可以攞嚟模仿人類同第啲動物所展現嘅智能,達致人工智能想做嘅嘢。
硬件問題 編輯
廿一世紀初,大同有效嘅人工神經網絡要求相當多嘅運算資源[101]。
動物嘅腦嘅能量效率好高,例如普通大人嘅腦平均用大約 20 瓦咁多嘅能量;相比之下,廿一世紀初嘅 GPU 閒閒地要用幾百瓦嘅能量,而且能量流失好勁,行起上嚟產生嘅廢熱可以令塊 GPU 熱到攝氏 50 至 80 度,唔似得人腦噉能夠維持喺攝氏 37 至 38 度左右。由此可見,廿一世紀初嘅人工神經網絡用起能量上嚟效率苲過生物神經網絡好多,而事實係,到咗 2019 年為止都仲係冇方法用近似生物神經網絡嘅能量效率嘅方法做一個模擬人腦嘅人工神經網絡[17][101]。
有電腦科學家指出,廿一世紀初人工神經網絡之所以會再興起,好大程度上係因為電腦硬件上嘅進步:喺 1991 至 2015 年間,GPU 嘅運算力提高咗成 100 萬倍咁多,令到反向傳播算法變成有可能-打前嘅電腦因為運算速度低,可能同一個得幾粒細胞嘅神經網絡做反向傳播都要做幾日咁耐,所以實際應用上根本冇用[102]。而運算能力上嘅進步令到本嚟要用成幾個月先做完嘅人工神經網絡學習喺幾日之間就做得嗮[101][103]。
應用 編輯
人工神經網絡能夠模擬輸入同輸出之間一啲非線性嘅關係,所以好多時都能夠有效噉對現實世界嘅現象做出預測。比較普通嘅前饋同遞迴神經網絡都有好廣泛嘅用途:
- 醫療診斷:喺醫療上,人工神經網絡能夠幫手對病人做診斷。曉寫程式嘅醫療人員可以製作一啲人工神經網絡,輸入設做「病徵」,而輸出設做「診斷」(兩者都用某啲數字代表),再用已有嘅醫療數據俾啲網絡做監督式學習,就會造出能夠基於病徵預測「診斷應該係乜」嘅網絡。事實係,廿一世紀初嘅學界經已有曉有效噉基於病人資訊診斷肺癌[104]、大腸癌[105]同前列腺癌[106]等病症嘅神經網絡。有啲神經網絡仲曉靠有關細胞形狀嘅數據嚟分辨邊啲癌細胞係比較惡性(大機會散佈去身體第啲部份)嘅[107][108]。
- 電腦保安:電腦保安係一個研究點樣確保電腦同互聯網安全嘅領域,包含咗對電腦病毒等惡意程式嘅應付同埋探測黑客等等嘅課題。人工神經網絡嘅技術可以用嚟教電腦分辨邊啲程式係惡意程式[109]、搵出搞破壞嘅人(例如係黑客)嘅戶口[110]、探測邊啲網址具有威脅性[111]、同埋探測信用卡詐騙呀噉[112];例如用一個監督式學習嘅神經網絡,輸入設做個網站嘅特徵—「有冇嘗試攞個瀏覽者嘅 IP」、「有冇彈視窗出嚟」、或者「有冇啲連咗去已知惡意網站嘅連結」等等—而輸出設做「係咪惡意網站」[110]。
- 遊戲控制:有遊戲人工智能方面嘅研究者指出,人工神經網絡能夠相當準確噉預測一個玩家有幾鍾意隻遊戲(遊戲特性做網絡輸入,玩家鍾意程度做輸出);於是佢哋就提議一個做法,將一隻電子遊戲嘅遊戲程式編寫成喺每一個時間點,都會用一個神經網絡按遊戲參數估計玩家有幾享受隻遊戲,並且計算享受度隨遊戲參數嘅偏導數,得知享受度會點樣隨遊戲參數變化,然後個程式會按呢份資訊調整隻遊戲;實驗結果顯示,噉嘅做法能夠提升一隻遊戲嘅玩家享受程度[113]。
- 結構分析:喺建築學同結構工程學上,設計一棟建築物嗰陣需要分析吓棟嘢能唔能夠穩陣噉企到喺度,而建築師等嘅人員可以將有關過去嘅建築物嘅數據攞嚟幫個神經網絡做監督式學習-例如輸入做棟建築物嘅形狀同幾何特徵,而輸出就設做棟嘢五十年內冧嘅機率,用嚟預測一楝建築物有幾穩陣[114][115][116]。
- 其他:
- ... 等等。
領域 編輯
睇埋 編輯
註釋 編輯
歐詞 編輯
- ↑ neuron
- ↑ artificial neuron
- ↑ weight
- ↑ bias
- ↑ activation level
- ↑ threshold value
- ↑ identity function
- ↑ propagation function
- ↑ weight vector
- ↑ input vector
- ↑ scalar
- ↑ linear function
- ↑ sigmoid function
- ↑ multilayer feedforward network
- ↑ input layer
- ↑ hidden layer
- ↑ nonlinearity
- ↑ output layer
- ↑ feedforward network
- ↑ recurrent network
- ↑ natural language
- ↑ learning rule
- ↑ training set
- ↑ error function
- ↑ backpropagation
- ↑ stochastic gradient descent
- ↑ partial derivative
- ↑ optimization
- ↑ gradient
- ↑ batch training
- ↑ batch size
- ↑ learning rate
- ↑ momentum
- ↑ supervised learning
- ↑ pattern recognition
- ↑ regression analysis
- ↑ binary
- ↑ unsupervised learning
- ↑ cluster analysis
- ↑ reinforcement learning
- ↑ agent
- ↑ action
- ↑ environment
- ↑ interpreter
- ↑ Q-learning
- ↑ Q-factor
- ↑ convolutional neural network
- ↑ preprocessing
- ↑ Big Data
- ↑ deep belief network
- ↑ restricted Boltzmann machine;RBM
- ↑ long short-term memory,LSTM
- ↑ gated neuron
- ↑ gate
- ↑ output gate
- ↑ input gate
- ↑ forget gate
- ↑ black box
- ↑ explainability
- ↑ Hopfield network
文獻 編輯
- Bhadeshia H. K. D. H. (1999). "'Neural Networks in Materials Science" (PDF). ISIJ International. 39 (10): 966–979. doi:10.2355/isijinternational.39.966.
- Bishop, Christopher (1995). Neural networks for pattern recognition. Clarendon Press. ISBN 978-0198538493. OCLC 33101074.
- Borgelt, Christian (2003). Neuro-Fuzzy-Systeme: von den Grundlagen künstlicher Neuronaler Netze zur Kopplung mit Fuzzy-Systemen. Vieweg. ISBN 9783528252656. OCLC 76538146.
- Coolen, A. C. (1998). A beginner's guide to the mathematics of neural networks (PDF). In Concepts for Neural Networks (pp. 13-70). Springer, London.
- Cybenko, G.V. (2006). "Approximation by Superpositions of a Sigmoidal function". In van Schuppen, Jan H. (ed.). Mathematics of Control, Signals, and Systems. Springer International. pp. 303–314.
- Dewdney, A. K. (1997). Yes, we have no neutrons: an eye-opening tour through the twists and turns of bad science. New York: Wiley. ISBN 9780471108061. OCLC 35558945.
- Duda, Richard O.; Hart, Peter Elliot; Stork, David G. (2001). Pattern classification (2 ed.). Wiley. ISBN 978-0471056690. OCLC 41347061.
- Egmont-Petersen, M.; de Ridder, D.; Handels, H. (2002). "Image processing with neural networks – a review". Pattern Recognition. 35 (10): 2279–2301. CiteSeerX 10.1.1.21.5444. doi:10.1016/S0031-3203(01)00178-9.
- Fahlman, S.; Lebiere, C (1991). "The Cascade-Correlation Learning Architecture" (PDF).
- created for National Science Foundation, Contract Number EET-8716324, and Defense Advanced Research Projects Agency (DOD), ARPA Order No. 4976 under Contract F33615-87-C-1499.
- Gurney, Kevin (1997). An introduction to neural networks. UCL Press. ISBN 978-1857286731. OCLC 37875698.
- Haykin, Simon S. (1999). Neural networks: a comprehensive foundation. Prentice Hall. ISBN 978-0132733502. OCLC 38908586.
- Hertz, J.; Palmer, Richard G.; Krogh, Anders S. (1991). Introduction to the theory of neural computation. Addison-Wesley. ISBN 978-0201515602. OCLC 21522159.
- Information theory, inference, and learning algorithms. Cambridge University Press. 25 September 2003. ISBN 9780521642989. OCLC 52377690.
- Krishnan, G. P., Tadros, T., Ramyaa, R., & Bazhenov, M. (2019). Biologically inspired sleep algorithm for artificial neural networks (PDF). arXiv preprint arXiv:1908.02240.
- Kruse, Rudolf; Borgelt, Christian; Klawonn, F.; Moewes, Christian; Steinbrecher, Matthias; Held, Pascal (2013). Computational intelligence: a methodological introduction. Springer. ISBN 9781447150121. OCLC 837524179.
- Lawrence, Jeanette (1994). Introduction to neural networks: design, theory and applications. California Scientific Software. ISBN 978-1883157005. OCLC 32179420.
- MacKay, David, J.C. (2003). Information Theory, Inference, and Learning Algorithms (PDF). Cambridge University Press. ISBN 9780521642989.
- Masters, Timothy (1994). Signal and image processing with neural networks: a C++ sourcebook. J. Wiley. ISBN 978-0471049630. OCLC 29877717.
- Misra, J., & Saha, I. (2010). Artificial neural networks in hardware: A survey of two decades of progress (PDF). Neurocomputing, 74(1-3), 239-255.
- Ripley, Brian D. (2007). Pattern Recognition and Neural Networks. Cambridge University Press. ISBN 978-0-521-71770-0.
- Siegelmann, H.T.; Sontag, Eduardo D. (1994). "Analog computation via neural networks". Theoretical Computer Science. 131 (2): 331–360. doi:10.1016/0304-3975(94)90178-3.
- Smith, Murray (1993). Neural networks for statistical modeling. Van Nostrand Reinhold. ISBN 978-0442013103. OCLC 27145760.
- Wasserman, Philip D. (1993). Advanced methods in neural computing. Van Nostrand Reinhold. ISBN 978-0442004613. OCLC 27429729.
攷 編輯
- ↑ "Artificial Neural Networks as Models of Neural Information Processing | Frontiers Research Topic". Retrieved 2018-02-20.
- ↑ Russell, Stuart J.; Norvig, Peter (2010). Artificial Intelligence A Modern Approach. Prentice Hall. p. 578.
- ↑ Gardner, M. W., & Dorling, S. R. (1998). Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences. Atmospheric environment, 32(14-15), 2627-2636.
- ↑ Omidvar, O., & Elliott, D. L. (1997). Neural systems for control. Elsevier.
- ↑ Bryson, Arthur Earl (1969). Applied Optimal Control: Optimization, Estimation and Control. Blaisdell Publishing Company or Xerox College Publishing. p. 481.
- ↑ The Machine Learning Dictionary - activation level 互聯網檔案館嘅歸檔,歸檔日期2018年8月26號,..
- ↑ 7.0 7.1 Learning process of a neural network 互聯網檔案館嘅歸檔,歸檔日期2021年2月11號,.. Towards Data Science.
- ↑ Tahmasebi; Hezarkhani (2012). "A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation". Computers & Geosciences. 42: 18–27
- ↑ Ivakhnenko, A. G.; Grigorʹevich Lapa, Valentin (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co.
- ↑ Akira Hirose, Shotaro Yoshida (2012). "Generalization Characteristics of Complex-valued Feedforward Neural Networks in Relation to Signal Coherence". IEEE TNNLS, 23(4): 541-551.
- ↑ Forrest M.D. (April 2015). "Simulation of alcohol action upon a detailed Purkinje neuron model and a simpler surrogate model that runs >400 times faster". BMC Neuroscience. 16 (27): 27.
- ↑ Marcus, Gary F. (2001). The Algebraic Mind: Integrating Connectionism and Cognitive Science (Learning, Development, and Conceptual Change). Cambridge, Massachusetts: MIT Press. pp. 27-28.
- ↑ Herz, A. V., Gollisch, T., Machens, C. K., & Jaeger, D. (2006). Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science, 314(5796), 80-85.
- ↑ Neuringer, M., Connor, W. E., Lin, D. S., Barstad, L., & Luck, S. (1986). Biochemical and functional effects of prenatal and postnatal omega 3 fatty acid deficiency on retina and brain in rhesus monkeys. Proceedings of the National Academy of Sciences, 83(11), 4021-4025.
- ↑ Hubel, D. H., & Wiesel, T. N. (1962). Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. The Journal of physiology, 160(1), 106-154.
- ↑ 16.0 16.1 16.2 16.3 16.4 Zell, Andreas (1994). "chapter 5.2". Simulation Neuronaler Netze [Simulation of Neural Networks] (in German) (1st ed.). Addison-Wesley.
- ↑ 17.0 17.1 17.2 17.3 The differences between Artificial and Biological Neural Networks. Towards Data Science.
- ↑ Hagan, Martin. Neural Network Design. PWS Publishing Company. 1996.
- ↑ Abbod, Maysam F (2007). "Application of Artificial Intelligence to the Management of Urological Cancer". The Journal of Urology. 178 (4): 1150-1156.
- ↑ Dawson, Christian W (1998). "An artificial neural network approach to rainfall-runoff modelling". Hydrological Sciences Journal. 43 (1): 47-66.
- ↑ Multi-Layer Neural Networks with Sigmoid Function— Deep Learning for Rookies (2). Towards Data Science.
- ↑ 22.0 22.1 22.2 Schmidhuber, J. (2015). "Deep Learning in Neural Networks: An Overview". Neural Networks. 61: 85-117.
- ↑ Ivakhnenko, A. G. (1973). Cybernetic Predicting Devices. CCM Information Corporation.
- ↑ Wanas, N., Auda, G., Kamel, M. S., & Karray, F. A. K. F. (1998, May). On the optimal number of hidden nodes in a neural network. In IEEE Canadian Conference on Electrical and Computer Engineering (Vol. 2, pp. 918-921).
- ↑ Auer, Peter; Harald Burgsteiner; Wolfgang Maass (2008). "A learning rule for very simple universal approximators consisting of a single layer of perceptrons". Neural Networks. 21 (5): 786–795.
- ↑ "2.3.4 Single-Layer Network". 原著喺2018年9月15號歸檔. 喺2018年8月30號搵到.
- ↑ The mostly complete chart of Neural Networks, explained. Towards Data Science.
- ↑ Siegelmann, H.T.; Sontag, E.D. (1991). "Turing computability with neural nets". Appl. Math. Lett. 4 (6): 77–80.
- ↑ 29.0 29.1 Sak, Hasim; Senior, Andrew; Beaufays, Francoise (2014). "Long Short-Term Memory recurrent neural network architectures for large scale acoustic modeling 互聯網檔案館嘅歸檔,歸檔日期2018年4月24號,." (PDF).
- ↑ How do Artificial Neural Networks learn? 互聯網檔案館嘅歸檔,歸檔日期2018年6月5號,..
- ↑ Haykin, S. S., Haykin, S. S., Haykin, S. S., Elektroingenieur, K., & Haykin, S. S. (2009). Neural networks and learning machines (Vol. 3). Upper Saddle River: Pearson education.
- ↑ Jain, A. K., Mao, J., & Mohiuddin, K. M. (1996). Artificial neural networks: A tutorial. Computer, (3), 31-44.
- ↑ Nielsen, Michael A. (2015). "Chapter 6". Neural Networks and Deep Learning.
- ↑ Kelley, Henry J. (1960). "Gradient theory of optimal flight paths". ARS Journal. 30 (10): 947–954.
- ↑ Mei, Song (2018). "A mean field view of the landscape of two-layer neural networks". Proceedings of the National Academy of Sciences. 115 (33): E7665–E7671.
- ↑ Dreyfus, Stuart (1962). "The numerical solution of variational problems". Journal of Mathematical Analysis and Applications. 5 (1): 30-45.
- ↑ Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (1986). "Learning representations by back-propagating errors". Nature. 323 (6088): 533-536.
- ↑ Dreyfus, Stuart (1973). "The computational solution of optimal control problems with time lag". IEEE Transactions on Automatic Control. 18 (4): 383–385.
- ↑ Dreyfus, Stuart E. (1990-09-01). "Artificial neural networks, back propagation, and the Kelley-Bryson gradient procedure". Journal of Guidance, Control, and Dynamics. 13 (5): 926–928.
- ↑ Huang, Guang-Bin; Zhu, Qin-Yu; Siew, Chee-Kheong (2006). "Extreme learning machine: theory and applications". Neurocomputing. 70 (1): 489-501.
- ↑ Widrow, Bernard; et al. (2013). "The no-prop algorithm: A new learning algorithm for multilayer neural networks". Neural Networks. 37: 182-188.
- ↑ Werbos, Paul J. (1994). The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting. New York, NY: John Wiley & Sons, Inc.
- ↑ Eiji Mizutani, Stuart Dreyfus, Kenichi Nishio (2000). On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application. Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN 2000), Como Italy, July 2000.
- ↑ Arthur E. Bryson (1961, April). A gradient method for optimizing multi-stage allocation processes. In Proceedings of the Harvard Univ. Symposium on digital computers and their applications.
- ↑ 45.0 45.1 What is the Difference Between a Batch and an Epoch in a Neural Network? 互聯網檔案館嘅歸檔,歸檔日期2019年6月20號,..
- ↑ Understanding Neural Network Batch Training: A Tutorial 互聯網檔案館嘅歸檔,歸檔日期2019年6月20號,..
- ↑ How to Configure the Learning Rate Hyperparameter When Training Deep Learning Neural Networks 互聯網檔案館嘅歸檔,歸檔日期2019年6月20號,..
- ↑ Hwang, S. K. J. (1988). An algebraic projection analysis for optimal hidden units size and learning rates in back-propagation learning. In IEEE... International Conference on Neural Networks (Vol. 1). SOS Printing.
- ↑ Reed, R., & MarksII, R. J. (1999). Neural smithing: supervised learning in feedforward artificial neural networks. Mit Press. p. 72.
- ↑ 50.0 50.1 50.2 50.3 Zeiler, M. D. (2012). ADADELTA: an adaptive learning rate method. arXiv preprint arXiv:1212.5701.
- ↑ Li, Y.; Fu, Y.; Li, H.; Zhang, S. W. (1 June 2009). The Improved Training Algorithm of Back Propagation Neural Network with Self-adaptive Learning Rate. 2009 International Conference on Computational Intelligence and Natural Computing. 1. pp. 73–76.
- ↑ D.E. Rumelhart, G.E. Hinton, and R.J. Williams, “Learning representations by back-propagating errors,” Nature, vol. 323, pp. 533-536, 1986.
- ↑ 53.0 53.1 53.2 Ojha, Varun Kumar; Abraham, Ajith; Snášel, Václav (2017-04-01). "Metaheuristic design of feedforward neural networks: A review of two decades of research". Engineering Applications of Artificial Intelligence. 60: 97–116.
- ↑ Ting Qin, et al. "A learning algorithm of CMAC based on RLS." Neural Processing Letters 19.1 (2004): 49-61.
- ↑ M.R. Smith and T. Martinez (2011). "Improving Classification Accuracy by Identifying and Removing Instances that Should Be Misclassified". Proceedings of International Joint Conference on Neural Networks (IJCNN 2011). pp. 2690-2697.
- ↑ Looney, C. G. (1997). Pattern recognition using neural networks: theory and algorithms for engineers and scientists (pp. 171-172). New York: Oxford University Press.
- ↑ Tu, J. V. (1996). Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. Journal of clinical epidemiology, 49(11), 1225-1231.
- ↑ Cancer Detection - MATLAB Example[失咗效嘅鏈].
- ↑ Menéndez, L. Á., de Cos Juez, F. J., Lasheras, F. S., & Riesgo, J. Á. (2010). Artificial neural networks applied to cancer detection in a breast screening programme. Mathematical and Computer Modelling, 52(7-8), 983-991.
- ↑ Milani, C., & Jadavji, N. M. (2017). Solving cancer: The use of artificial neural networks in cancer diagnosis and treatment. Journal of Young Investigators, 33(4).
- ↑ Introduction to Unsupervised Learning 互聯網檔案館嘅歸檔,歸檔日期2019年6月22號,..
- ↑ 62.0 62.1 62.2 Unsupervised Learning and Data Clustering. Towards Data Science.
- ↑ Unsupervised learning - MathWorks.
- ↑ 64.0 64.1 Dostál, P., & Pokorný, P. (2009). Cluster analysis and neural network. In 17th Annual Conference Proceedings on Technical Computing Prague (pp. 131-57).
- ↑ Dominic, S.; Das, R.; Whitley, D.; Anderson, C. (July 1991). "Genetic reinforcement learning for neural networks". IJCNN-91-Seattle International Joint Conference on Neural Networks. IJCNN-91-Seattle International Joint Conference on Neural Networks. Seattle, Washington, USA: IEEE.
- ↑ Hoskins, J.C.; Himmelblau, D.M. (1992). "Process control via artificial neural networks and reinforcement learning". Computers & Chemical Engineering. 16 (4): 241–251.
- ↑ Bertsekas, D.P.; Tsitsiklis, J.N. (1996). Neuro-dynamic programming. Athena Scientific. p. 512.
- ↑ 68.0 68.1 68.2 NEURAL NETWORKS AND REINFORCEMENT LEARNING 互聯網檔案館嘅歸檔,歸檔日期2018年10月24號,. (PDF).
- ↑ Miller, W. T., Werbos, P. J., & Sutton, R. S. (Eds.). (1995). Neural networks for control. MIT press.
- ↑ Tsitsiklis, J., (1994), 'Asynchronous Stochastic Approximation and Q-learning. Machine Learning'.
- ↑ Sengupta, Nandini; Sahidullah, Md; Saha, Goutam (August 2016). "Lung sound classification using cepstral-based statistical features". Computers in Biology and Medicine. 75 (1): 118–129.
- ↑ Fukushima, K. (1980). "Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position". Biol. Cybern. 36 (4): 193–202.
- ↑ Ran, Lingyan; Zhang, Yanning; Zhang, Qilin; Yang, Tao (12 June 2017). "Convolutional Neural Network-Based Robot Navigation Using Uncalibrated Spherical Images". Sensors. 17 (6): 1341.
- ↑ 74.0 74.1 Image Classification using Deep Neural Networks — A beginner friendly approach using TensorFlow 互聯網檔案館嘅歸檔,歸檔日期2019年6月24號,.. Towards Data Science.
- ↑ Parisi, R., Di Claudio, E. D., Lucarelli, G., & Orlandi, G. (1998, May). Car plate recognition by neural networks and image processing. In ISCAS'98. Proceedings of the 1998 IEEE International Symposium on Circuits and Systems (Cat. No. 98CH36187) (Vol. 3, pp. 195-198). IEEE.
- ↑ Egmont-Petersen, M., de Ridder, D., & Handels, H. (2002). Image processing with neural networks—a review. Pattern recognition, 35(10), 2279-2301.
- ↑ LeCun et al., "Backpropagation Applied to Handwritten Zip Code Recognition," Neural Computation, 1, pp. 541–551, 1989.
- ↑ Szegedy, Christian; Liu, Wei; Jia, Yangqing; Sermanet, Pierre; Reed, Scott; Anguelov, Dragomir; Erhan, Dumitru; Vanhoucke, Vincent; Rabinovich, Andrew (2014). Going Deeper with Convolutions. Computing Research Repository.
- ↑ Image Classifier - Cats vs Dogs 互聯網檔案館嘅歸檔,歸檔日期2019年4月21號,.. Medium.
- ↑ All the Steps to Build your first Image Classifier (with code). Towards Data Science.
- ↑ J. Gantz and D. Reinsel, Extracting Value from Chaos. Hopkinton, MA, USA: EMC, Jun. 2011.
- ↑ Larochelle, Hugo; Erhan, Dumitru; Courville, Aaron; Bergstra, James; Bengio, Yoshua (2007). An Empirical Evaluation of Deep Architectures on Problems with Many Factors of Variation. Proceedings of the 24th International Conference on Machine Learning. ICML '07. New York, NY, USA: ACM. pp. 473–480.
- ↑ Deep Learning : Deep Belief Network Fundamentals[失咗效嘅鏈]. Medium.
- ↑ Hinton, G. E. (2010). "A Practical Guide to Training Restricted Boltzmann Machines". Tech. Rep. UTML TR 2010-003.
- ↑ Bengio, Y. (2009). "Learning Deep Architectures for AI". Foundations and Trends in Machine Learning. 2 (1): 1-127.
- ↑ Al-Jarrah, O. Y., Yoo, P. D., Muhaidat, S., Karagiannidis, G. K., & Taha, K. (2015). Efficient machine learning for big data: A review. Big Data Research, 2(3), 87-93.
- ↑ 87.0 87.1 87.2 87.3 Sepp Hochreiter; Jürgen Schmidhuber (1997). "Long short-term memory". Neural Computation. 9(8): 1735–1780.
- ↑ Bayer, Justin; Wierstra, Daan; Togelius, Julian; Schmidhuber, Jürgen (14 September 2009). Evolving Memory Cell Structures for Sequence Learning (PDF). Artificial Neural Networks – ICANN 2009. Lecture Notes in Computer Science. 5769. Springer, Berlin, Heidelberg. pp. 755–764.
- ↑ Fernández, Santiago; Graves, Alex; Schmidhuber, Jürgen (2007). "Sequence labelling in structured domains with hierarchical recurrent neural networks". In Proc. 20th Int. Joint Conf. On Artificial Intelligence, Ijcai 2007: 774–779.
- ↑ Graves, Alex; Fernández, Santiago; Gomez, Faustino (2006). "Connectionist temporal classification: Labelling unsegmented sequence data with recurrent neural networks". In Proceedings of the International Conference on Machine Learning, ICML 2006: 369–376.
- ↑ Gers, F. A., Schraudolph, N. N., & Schmidhuber, J. (2002). Learning precise timing with LSTM recurrent networks. Journal of machine learning research, 3(Aug), 115-143.
- ↑ 92.0 92.1 THE BLACK BOX PROBLEM CLOSES IN ON NEURAL NETWORKS 互聯網檔案館嘅歸檔,歸檔日期2018年6月22號,.. The Next Platform.
- ↑ Trust, and don’t verify: the AI black box problem 互聯網檔案館嘅歸檔,歸檔日期2018年7月30號,.. Medium.
- ↑ Peres, D. J.; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. (1 October 2015). "Significant wave height record extension by neural networks and reanalysis wind data". Ocean Modelling. 94: 128–140.
- ↑ Dwarakish, G. S.; Rakshith, Shetty; Natesan, Usha (2013). "Review on Applications of Neural Network in Coastal Engineering". Artificial Intelligent Systems and Machine Learning. 5 (7): 324–331.
- ↑ Dewdney, A. K. (1 April 1997). Yes, we have no neutrons: an eye-opening tour through the twists and turns of bad science. Wiley. p. 82.
- ↑ Holzinger, Andreas; Plass, Markus; Holzinger, Katharina; Crisan, Gloria Cerasela; Pintea, Camelia-M.; Palade, Vasile (3 August 2017). "A glass-box interactive machine learning approach for solving NP-hard problems with the human-in-the-loop". arXiv:1708.01104
- ↑ Adrian, Edward D. (1926). "The impulses produced by sensory nerve endings". The Journal of Physiology. 61 (1): 49-72.
- ↑ Kandel ER, Schwartz JH, Jessell TM (2003). "Chapter 55: The formation and regeneration of synapses". Principles of Neural Science (fourth ed.). Cambridge: McGrawHill.
- ↑ Crick, Francis (1989). "The recent excitement about neural networks". Nature. 337(6203): 129–132.
- ↑ 101.0 101.1 101.2 Edwards, Chris (25 June 2015). "Growing pains for deep learning". Communications of the ACM. 58 (7): 14–16.
- ↑ Schmidhuber, Jürgen (2015). "Deep learning in neural networks: An overview". Neural Networks. 61: 85–117.
- ↑ "A Survey of FPGA-based Accelerators for Convolutional Neural Networks", NCAA, 2018.
- ↑ Ganesan, N. "Application of Neural Networks in Diagnosing Cancer Disease Using Demographic Data 互聯網檔案館嘅歸檔,歸檔日期2019年6月26號,." (PDF). International Journal of Computer Applications.
- ↑ Bottaci, Leonardo. "Artificial Neural Networks Applied to Outcome Prediction for Colorectal Cancer Patients in Separate Institutions 互聯網檔案館嘅歸檔,歸檔日期2018年11月23號,." (PDF). The Lancet.
- ↑ Djavan, B., Remzi, M., Zlotta, A., Seitz, C., Snow, P., & Marberger, M. (2002). Novel artificial neural network for early detection of prostate cancer. Journal of Clinical Oncology, 20(4), 921-929.
- ↑ Alizadeh, Elaheh; Lyons, Samanthe M; Castle, Jordan M; Prasad, Ashok (2016). "Measuring systematic changes in invasive cancer cell shape using Zernike moments". Integrative Biology. 8 (11): 1183–1193.
- ↑ Lyons, Samanthe (2016). "Changes in cell shape are correlated with metastatic potential in murine". Biology Open. 5(3): 289–299.
- ↑ Nix, R.; Zhang, J. (May 2017). "Classification of Android apps and malware using deep neural networks". 2017 International Joint Conference on Neural Networks (IJCNN): 1871–1878.
- ↑ 110.0 110.1 "Machine Learning: Detecting malicious domains with Tensorflow". The Coruscan Project.
- ↑ "Detecting Malicious URLs 互聯網檔案館嘅歸檔,歸檔日期2019年7月14號,.". The systems and networking group at UCSD.
- ↑ Ghosh, S., & Reilly, D. L. (1994, January). Credit card fraud detection with a neural-network. In System Sciences, 1994. Proceedings of the Twenty-Seventh Hawaii International Conference on (Vol. 3, pp. 621-630). IEEE.
- ↑ Yannakakis, G. N., & Hallam, J. (2009). Real-time game adaptation for optimizing player satisfaction. IEEE Transactions on Computational Intelligence and AI in Games, 1(2), 121-133.
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (28 August 2017). "Deep Learning for Accelerated Reliability Analysis of Infrastructure Networks". Computer-Aided Civil and Infrastructure Engineering. 33 (6): 443–458.
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (2018). "'Accelerating Stochastic Assessment of Post-Earthquake Transportation Network Connectivity via Machine-Learning-Based Surrogates". Transportation Research Board 97th Annual Meeting.
- ↑ Díaz, E.; Brotons, V.; Tomás, R. (September 2018). "Use of artificial neural networks to predict 3-D elastic settlement of foundations on soils with inclined bedrock". Soils and Foundations. 58 (6): 1414–1422.
- ↑ Silver, David, et al. "Mastering the game of Go with deep neural networks and tree search." Nature, 529.7587 (2016): 484.
- ↑ Sengupta, Nandini; Sahidullah, Md; Saha, Goutam (August 2016). "Lung sound classification using cepstral-based statistical features". Computers in Biology and Medicine. 75 (1): 118–129.
- ↑ Choy, Christopher B., et al. "3d-r2n2: A unified approach for single and multi-view 3d object reconstruction." European conference on computer vision. Springer, Cham, 2016.
- ↑ French, Jordan (2016). "The time traveller's CAPM". Investment Analysts Journal. 46 (2): 81–96.
- ↑ Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
拎 編輯
- 對神經網絡嘅一個簡短介紹 (英文),PDF 快勞,一本 250 頁長嘅大學教科書,教有關人工神經網絡嘅基本知識。
- An Introduction to Deep Neural Networks (英文)
- A Tutorial of Neural Network in Excel (英文)
- YouTube上面嘅MIT course on Neural Networks
- A Concise Introduction to Machine Learning with Artificial Neural Networks (英文)
- Neural Networks for Machine Learning – a course by Geoffrey Hinton (英文)
- Deep Learning (英文)
- Interactive visualization of neural work (英文)
- Neural Networks and Deep Learning (英文)




